Стабилност на усилвателите с обратна връзка
Обобщавайки резултатите, получени в предишните раздели, може да се отбележи, че в случай на малки фазови измествания в цикъла, отрицателната обратна връзка има ефективно стабилизиращо и линеаризиращо свойство, води до значително намаляване на всички видове изкривявания и ви позволява да променяте стойностите на входното и изходното съпротивление в необходимата посока. Почти всички благоприятни ефекти на FOS са пропорционални на дълбочината на обратната връзкаF=1+Kb.
Тъй като в случай на верига за пасивна обратна връзка, която се използва главно при конструирането на стабилни усилвателни устройства, b £ 1, увеличаването на дълбочината на обратната връзка е възможно само чрез увеличаване на усилването на оригиналния усилвателK, което се постига чрез въвеждане на голям брой последователно свързани усилвателни етапи.
В допълнение към значителното усложнение на веригата,голям брой етапи води до увеличаване на фазовото изместване в обратната връзка, което в допълнение към намаляването на ефективността на FOS може да доведе при определени условия до такова нежелано явление катофалшиво генериране.
Фалшиво генериранее появата на изхода на усилвателя на сигнал, чиито параметри не зависят от входния сигнал, т.е. фалшив генериран сигнал може да възникне и при липса на входен сигнал. Физически, феноменът на паразитното генериране възниква поради прехвърлянето на енергия от изхода на усилвателя през веригата за обратна връзка към неговите управляващи клеми, т.е. това е типично за системи с обратна връзка. Обикновено напрежението на паразитното генериране е много по-високо от нивото на собствения шум, което практически изключва нормалното функциониране на усилващото устройство. При наличие на паразитна генерация усилвателят се нарича нестабилен.
Устойчивостта е налицев повечето случаи най-трудният проблем за решаване в процеса на проектиране на усилватели с дълбока обратна връзка.
Тъй като паразитното генериране се определя от вътрешните процеси, протичащи в усилвателя, стабилността се оценява от вида на решението на линеаризираното диференциално уравнение с нулевата дясна част (т.е. при липса на външни смущения) - характеристично уравнение, което се определя от знаменателя на предавателната функцияKС ) или комплексния коефициент на предаване (jw).За усилвател с OOS
и характеристичното уравнение на усилвател с обратна връзка има формата
[1 + K(p) × b(p)] = [1 + T(p)] = 0.
Решението на такова уравнение се търси във вида
,
къдетоU(0) е началното условие;pi –корени на характеристичното уравнение.
Очевидно, ако характеристичното уравнение има поне един корен (проста или сложна спрегната двойка) с положителна реална част
тогава решението на характеристичното уравнение ще има един член с коефициент, нарастващ във времето
което показва нестабилността на усилвателя. Така,основният аналитичен признак за нестабилност на усилвателяе наличието на поне един корен от характеристичното уравнениес положителнареална част.
Има различни признаци, които ви позволяват да определите вида на корените, без да решавате характеристичното уравнение. Такива признаци се наричат критерии за устойчивост. Разработени са голям брой критерии.
По отношение на усилвателите, най-широко се използвачестотният критерий(критерий на Найкуист), който позволява да се прецени стабилността по формата на AFC ходографа на контурното усилванеT(jw).
Ходографът егеометричното място на точките, описани от края на вектораT(jw) на комплексната равнина, когато честотата се променя от 0 до ¥. Всяка честота в този диапазон съответства на вектор, чиято дължина е равна на модула, а ъгълът на въртене е фазата на контурното усилване (фиг. 5.17).
Съгласно честотния критерий, даден тук без доказателство, усилвателят ще бъде стабилен, ако ходографът на усилване на веригатаT(jw) не покрива точката с координати [–1,j0].
На фиг. 5.18, 5.19 показва ходографите на стабилни усилватели, а на фиг. 5.20 - нестабилен.
За практически най-често използваните усилватели с ходограф с формата, показана на фиг. 5.18 (с един фазов преход от 180°), честотният критерий означава, че при честотата, при която фазата на усилване на веригата достига 180°, модулът на усилване на веригата трябва да бъде по-малък от единица.
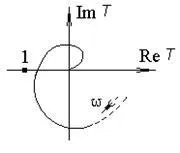 | 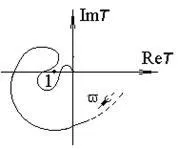 | 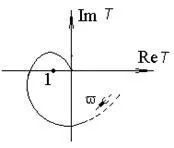 |
| Ориз. 5.18. Ходограф на стабилна система | Ориз. 5.19. Ходограф на стабилна система на Найкуист | Ориз. 5.20. Ходограф на нестабилна система |
На фиг. 5.21 и 5.22 са дадени съответно LAFC (честотна характеристика в логаритмична скала) и PFC за стабилни и нестабилни усилватели. Когато се разглежда LAFC, трябва да се има предвид, че lg(T=1)=0. Основното предимство на честотния критерий е възможността да се определи стабилността наексперименталноотстранените LAFC и PFCза отворена веригаобратна връзка.
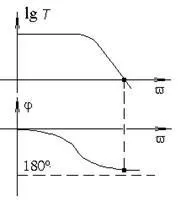 | 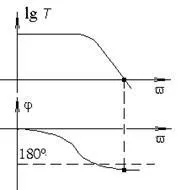 |
| Ориз. 5.21. LAFC и PFC на стабилна система | Ориз. 5.22. LAFC и PFC на нестабилна система |
Съвременните усилватели, особено в дизайна на микрочипове, имат толкова сложна структура, че за да получите точен анализописанието му е практически невъзможно; Именно при тези условия честотният метод за определяне на стабилността става важен.
Сигналът на изхода на нестабилен усилвател може да приеме големи стойности, при които усилвателят е в нелинеен режим, когато усилващите елементи на изходния етап се окажат неконтролируеми и през тях може да тече толкова голям ток, че елементът да се повреди. Честотният критерий дава възможност да се определи стабилността на усилвателяс отворена верига за обратна връзка, когато системата е стабилна, което също подчертава нейното достойнство.
5.2.6. Корекция на честотната характеристика за стабилност на усилвателя
Очевидно дизайнът на усилвател с OOS не може да завърши с просто изявление на факта на нестабилност.
Стабилността се постига чрез коригиране на оригиналната честотна характеристика.Както ще бъде показано по-долу, корекцията е придружена от значително стесняване на оригиналната честотна лента. В специалната литература се определя оптималната форма на коригираната LAFC, при която се постига минимално възможното стесняване на оригиналната честотна лента. Въпреки това, за прилагане на оптимална корекция са необходими сложниRLC-вериги с голям брой елементи. Ето защо на практика, особено в случай на усилватели на микросхеми, се използват най-простите коригиращи схеми типRC.
Най-простата корекция се постига чрез изкуствено увеличаване на времеконстантата на един или два етапа, например чрез свързване на кондензатор с определен капацитет към неговите изходни клеми. Увеличаването на времевата константа води до намаляване на граничната честота и в резултат на това до по-ранен спад в усилването на този етап и усилването на контура като цяло. Избран е корекционен капацитеттака че при честота, при която фазата достига 180 °, коефициентът на усилване на веригата има време да намалее до стойност, по-малка от единица. На фиг. 5.23 показва пример за такава корекция. Пунктираната линия показва оригиналния LFC на един етап (K1), усилването на контураTи PFC на усилването на контура. Както можете да видите, оригиналният усилвател е нестабилен, тъй като при честотатаf1, къдетоT= 1, фазата е по-голяма от 180°.
Плътните линии показват LFC на каскадатаK1 след нейната корекция, както и LFC и PFC на усилването на контура, като се вземе предвид корекциятаK1. Усилвателят стана стабилен, защото при новата честота на усилване на единичната веригаf ʹ1 фазата стана по-малка от 180°. 6 dB/oct LAFC наклон отбелязани на фиг. 5.23 катоn=1, при 18 dB/окт. –n =3.
Ясно се вижда, че стабилността чрез най-простата корекция е постигната поради значително стесняване на работната честотна лента.
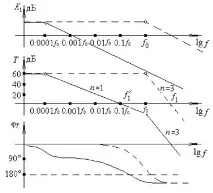
Ориз. 5.23. Първоначална (пунктирана линия) и коригирана LAFC φT
Тестови въпроси и задачи
1. Какво е обратна връзка? По какви причини се появява в усилвателя?
2. Направете блокови схеми на усилватели с обратна връзка:
а) серия по напрежение;
б) серия в течение;
в) паралелни по напрежение;
3. Посочете вида на обратната връзка [(за случаи а) и в)] по въпрос № 2, ако фазовото отместване между входното напрежение и напрежението на обратната връзка е: а) 0°; б) 100°; в) 180°; г) 270°; д) 360°.
4. Има усилвател със следните параметри:Rin=2 kOhm,Rout = 1 kOhm,Rn = 1 kOhm,Kхх = 1000. Използвайки OOS, изградете усилвател сRin.sv = 200 kOhm. Изчислете неговия изходен импеданс и усилване.
5. Какво е устойчивостусилвател? Какви методи за определяне на стабилността познавате?