Стойността на k за изчисляване на квадратното отклонение ( ) в амплитудата
За нашия пример стандартното отклонение по опростения метод: cm
Стойност на стандартното отклонение
1. С помощта на стандартното отклонение се извършваоценка на флуктуациятана вариационния ред. В симетрична вариационна серия в рамките на стойността на една сигма от стойността на средната аритметична, т.е. М ± 1 е 68,3% от общия вариант.
В рамките на две сигми (M ± 2 ) има 95,5% вариант, в интервала от три сигма (M ± 3 ) вече има 99,7% вариант на вариационната серия. Така при нормално разпределение почти целият вариационен ред се вписва в интервала от ±3 от средноаритметичната стойност. Последното е известно като "правилото на трите сигми".
2. Стандартното отклонение се използва заоценка на физическото развитие. Индивидите със стойности на черта в рамките на M ± 1 се оценяват като имащи нормално развитие и този интервал се счита за норма. Индивиди със стойност на черта в диапазона от +1 до +2 или -1 до -2 се оценяват като имащи развитие над или под нормалното, т.е. като поднорма. Ако вариантът е в диапазона от +2 до +3 или от -2 до -3, тогава такъв индивид се счита за висок или нисък (субаномалия).
3. Стандартното отклонение се използва заоценка на променливосттана няколко вариационни серии. В случаите, когато се сравняват редове, които имат една и съща система за измерване (например се характеризира само височина или телесно тегло), заключения могат да бъдат направени директно от стандартното отклонение. Въпреки това, когато се характеризират разнородни серии, когато стойностите на някои са представени в метри, други в килограми, трябва да се използва коефициентът на вариация:
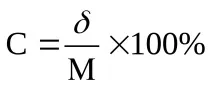
На практика се приемат следните критерииоценки на коефициента на вариация:
Нисък -ако стойността му не надвишава 10.0%;
Среден- ако стойността му варира от 10.0% до 20.0%;
Високо -, ако стойността му е по-голяма от 20,0%.
4. Стандартното отклонение се използва заоценка на надеждността на средните стойности, което ще бъде обсъдено по-долу.