Тема 2.10. Стабилност на компресирани пръти. Изчисления за устойчивост.

Познаване на условието за стабилност на компресираните пръти, формулите на Ойлер за определяне на критичната сила, емпиричните формули за изчисляване на критичното напрежение и критичната сила.

Да може да извършва изчисления за проверка на стабилността на компресирани пръти.

Процедура за изчисляване на стабилността

1. Получаване на информация за материала на пръта за определяне на крайната гъвкавост на пръта чрез изчисление или според таблицата:

където A е площта на напречното сечение; Jmin - минимален инерционен момент (от аксиален);

μ— намален коефициент на дължина.

3. Избор на изчислителни формули за определяне на критичната сила и критичното напрежение.

4. Проверка и устойчивост.

Когато се изчислява по формулата на Ойлер, условието за стабилност е:

F— действаща сила на натиск; [sу] е допустимият коефициент на стабилност.

При изчисляване по формулата на Ясински

къдетоa, bса проектни коефициенти в зависимост от материала (стойностите на коефициентите са дадени в таблица 36.1)

Ако условията за стабилност не са изпълнени, е необходимо да се увеличи площта на напречното сечение.

Понякога е необходимо да се определи границата на стабилност за дадено натоварване:

При проверка на стабилността изчислената издръжливост се сравнява с допустимата:

Примери за решаване на проблеми

Пример 1. Изчислете гъвкавостта на лентата. Кръгъл прът с диаметър 20 mm е фиксиран, както е показано на фиг. 37.1.

Решение

1. Гъвкавостта на пръта се определя по формулата

2. Определете минималния радиус на въртене на кръга.

Заместване на изрази заJminиA(секция с кръг)

1. Коефициент на намаляване на дължината за дадена схема на закрепванеμ= 0,5.
2. Гъвкавостта на пръта ще бъде

Пример 2. Как ще се промени критичната сила за пръта, ако се промени методът на фиксиране на краищата? Сравнете представените схеми (фиг. 37.2)

Решение

Критичната мощност ще се увеличи 4 пъти.

Пример 3. Как ще се промени критичната сила при изчисляване на устойчивостта, ако прътът с I-сечение (фиг. 37.3a, I-лъч № 12) се замени с правоъгълен прът със същата площ (фиг. 37.3b)? Останалите параметри на дизайна остават непроменени. Изчислението се извършва по формулата на Ойлер.

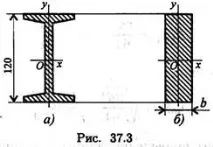
Решение

1. Определете ширината на сечението на правоъгълника, височината на сечението е равна на височината на сечението на I-лъча. Геометричните параметри на I-лъча № 12 съгласно GOST 8239-89 са както следва:

площ на сечениетоA1 =14.7 cm 2;

минимумът на аксиалните инерционни моменти.

По условие площта на правоъгълно сечение е равна на секционната площ на I-лъча. Определяме ширината на лентата на височина 12 см.

2. Определете минимума на аксиалните инерционни моменти.

3. Критичната сила се определя по формулата на Ойлер:

4. При равни други условия съотношението на критичните сили е равно на съотношението на минималните моменти на инерция:

5. По този начин стабилността на прът с участък от I-лъчи № 12 е 15 пъти по-висока от стабилността на прът с избрана правоъгълна секция.

Пример 4. Проверете стабилността на пръта. Пръчка с дължина 1 m се защипва в единия край, сечението е канал № 16, материалът е St3, границата на стабилност е три пъти. Прътът е натоварен със сила на натиск 82 kN (фиг. 37.4).

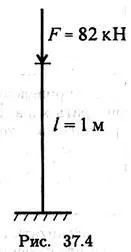
Решение

1. Определяме основните геометрични параметри на секцията на пръта съгласно GOST 8240-89. Канал № 16: площ на сечението 18,1 cm 2; минимален аксиален момент на сечението63,3 cm4; минималният радиус на въртене на сечението е r; n = 1,87 cm.

Изключителна гъвкавост за StZ материал λprev = 100.

Изчислена гъвкавост на пръта с дължинаl =1m = 1000mm

Изчисленият прът е прът с голяма гъвкавост, изчислението се извършва по формулата на Ойлер.

3. Допустимо натоварване на пръта

4. Условие за стабилност

82 kN 5 и σpc = 450 N/mm 2.

Решение

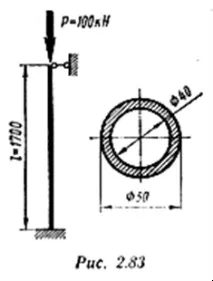
За анализ на стабилността трябва да се знае критичната сила за даден стелаж. Необходимо е да се установи по каква формула трябва да се изчисли критичната сила, т.е. необходимо е да се сравни гъвкавостта на стелажа с крайната гъвкавост на неговия материал.

Ние изчисляваме стойността на крайната гъвкавост, тъй като няма таблични данни за λ,prev за материала на стелажа:

За да определим гъвкавостта на изчислената стойка, изчисляваме геометричните характеристики на нейното напречно сечение:

Определете гъвкавостта на стелажа:

и се уверете, че λ [ny] с 5,2%.

Пример 2.87. Проверете здравината и стабилността на дадената прътова система (фиг. 2.86), Материалът на прътите е стомана St5 (σt \u003d 280 N / mm 2). Необходими коефициенти на безопасност: якост[n]= 1,8; стабилност[nу] =2.2. Пръчките имат кръгло напречно сечениеd1 = d2= 20 mm,d3 =28 mm.

Решение

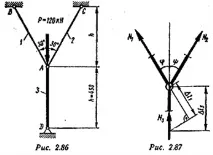
Изрязване на възела, в който прътите се събират, и съставяне на уравненията за равновесие за силите, действащи върху него (фиг. 2.86)

установяваме, че дадената система е статически неопределена (три неизвестни сили и две уравнения на статиката). Ясно е, че за да се изчисли якостта и стабилността на прътите, е необходимо да се знае величината на надлъжните сили, възникващи в техните напречни сечения, т.е. е необходимо да се разкрие статикатанеопределимост.

Съставяме уравнение на изместване въз основа на диаграмата на изместване (фиг. 2.87):

или, замествайки стойностите на промените в дължините на прътите, получаваме

Решавайки това уравнение заедно с уравненията на статиката, намираме:

Напрежения в напречните сечения на прътите1и2(виж фиг. 2.86):

Техният фактор на безопасност

За да се определи коефициентът на стабилност на прът3, е необходимо да се изчисли критичната сила и това изисква определяне на гъвкавостта на пръта, за да се реши коя формула да се използва за намиране наNKp.

Не намерихте това, което търсихте? Използвайте търсенето в Google на сайта:

---