Теорема на Лаплас

Детерминантата на квадратна матрица е равна на сумата от продуктите на елементите на всеки ред (колона) и техните алгебрични допълнения:

(*)

(разлагане по елементи отiти ред);

(**)

(разгъване по елементи отjта колона).

Нека проверим валидността на теоремата на Лаплас, като използваме примера за детерминанта на матрица от трети ред. Нека първо го разширим с елементите на първия ред

Което съвпада с дефиницията на детерминанта на матрица от трети ред.

Пример 1.Изчислете детерминанта от трети ред

използвайки своето елементно разширение на първия ред.

Решение.Намерете алгебричните допълнения на елементите от първия ред:

Сега, чрез теоремата на Лаплас, намираме детерминантата, използвайки формулата (*)

Пример 2.Изчислете детерминантата от предишния пример, като използвате нейното разлагане по елементите на втората колона.

Решение.Намерете алгебричните допълнения на елементите от втората колона:

Сега, използвайки формулата (**), намираме детерминантата на матрицата

Стойностите на първия и втория пример съвпадат, което означава, че можете да изберете разлагането по всеки ред или колона.

Пример 3.Изчислете детерминанта от четвърти ред на триъгълна матрица:

Решение:Нека разширим първата колона:

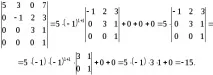
Значението на теоремата на Лаплас е, че тя ви позволява да намалите изчисляването на детерминанти отn-ти ред до изчисляване на детерминанта от по-малък ред, тоест (n-1)-ти ред.

За всяко число има реципрочна стойност, така че продуктът. Подобно понятие се въвежда и за квадратни матрици.

Дефиниция.Матрицата се нарича обратна на квадратна матрица, акоумножавайки тази матрица по дадената както отдясно, така и отляво, се получава матрицата за идентичност:

.

Само квадратна матрица може да има обратна, но не всяка квадратна матрица има обратна.

Дефиниция.Една матрица енеединична (неединична)ако , в противен случай матрицата се наричаединична (единична).

Теорема(необходимо и достатъчно условие за съществуването на обратна матрица).Обратна матрица съществува (и е уникална) тогава и само ако оригиналната матрица е неизродена (неособена) и се изчислява по формулата

,

където е присъединената матрица, състояща се от алгебрични допълнения на елементите на транспонираната матрица, т.е.

Необходимост. Нека матрицата има обратна, т.е. по свойството на 10 детерминанти имаме:, т.е.

Достатъчност. Позволявам . Помислете за квадратна матрица от n-ти ред, наречена присъединена, чиито елементи са алгебричните допълнения на елементите на матрицата, транспонирани в k. Тогава елементите на произведението на матриците се определят от правилото за умножение на матрици. Следователно матрицата B е диагонална, елементите на нейния главен диагонал са равни на детерминантата на оригиналната матрица. И произведението е равно на същата матрица B:.

Уникалностобратна матрица. Нека приемем, че има и такива матрици, че и, където матрицата се получава по формулата и равенствата са изпълнени. След това, умножавайки първото от тях вляво, получаваме:, откъдето, т.е. По същия начин, умножавайки второто равенство вдясно, получаваме. Уникалността е доказана.

---