Теория на Рамзи
Теорията на Рамзие клон на математиката, който изучава условията, при които трябва да се появи някакъв ред в произволно формирани математически обекти.
Има друго определение за числата на Рамзи.
Лесно се доказва, че тези определения са еквивалентни. Достатъчно е да се покаже, че двуцветна графика [math]K_n[/math] може да бъде уникално свързана с графика [math]G[/math] на [math]n[/math] върхове. Доста често дефиницията за числата на Рамзи се дава чрез проблема "приятели и непознати" [1] . Нека на парти всеки двама души могат да бъдат приятели или непознати, в общата форма на проблема трябва да намерите минималния брой хора, които трябва да вземете, така че поне [math]n[/math] души да са познати по двойки или поне [math]m[/math] хора да са непознати по двойки. Ако преформулираме този проблем по отношение на графики, тогава просто ще получим дефиницията на числото на Рамзи [math]r(n, m)[/math], представена по-рано.
Пример[редактиране]
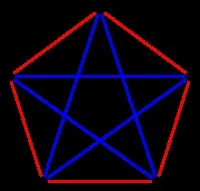
За да добием по-добра представа за природата на числата на Рамзи, нека вземем пример. Нека докажем, че [math]r(3,3) = 6[/math] . Представете си, че ръбовете [math]K_6[/math] са оцветени в два цвята: червен и син. Вземете върха [math]v[/math] . Този връх, както всички останали, е инцидентен с [math]5[/math] ръба, тогава, според принципа на Дирихле, поне три от тях са с един и същи цвят. За определеност приемаме, че поне [math]3[/math] ръбовете, свързващи върха [math]v[/math] с върховете [math]r[/math] , [math]s[/math] , [math]t[/math] , са сини. Ако поне едно от ребра [math]rs[/math] , [math]rt[/math] , [math]st[/math] е синьо, тогава графиката има син триъгълник (пълна графика на три върха), в противен случай, ако всички са червени, има червен триъгълник. Така [math]r(3,3) \leqslant6[/math] . За да докажем, че [math]r(3,3) = 6 [/math], ние представяме оцветяване на графиката [math]K_5[/math], където няма клик върху трите върха в син или червен цвят. Такова оцветяване е показано на фигурата вдясно. Ясно е, че няма нужда да се представят отделни оцветявания за [math] K_4[/math] , [math]K_3[/math] , тъй като е достатъчно да се вземат съответните подграфи на оцветеното [math]K_5[/math] .