тригонометричен кръг

В последната статия се запознахме стригонометричната окръжност и научихме как да намираме стойностите на синуса и косинуса на главните ъгли.

Какво ще кажете затангенс и котангенс ? Това е, за което ще говорим днес.

Къде са осите на тангенсите и котангенсите върху тригонометричната окръжност?

Допирателната ос е успоредна на синусовата ос (има същата посока като синусовата ос) и минава през точката (1; 0).

Котангенсната ос е успоредна на косинусовата ос (има същата посока като косинусовата ос) и минава през точката (0; 1).

На всяка от осите има такава верига от основни стойности на тангенс и котангенс: Защо е така?

Мисля, че лесно можете да го разберете сами. :) Можете да спорите различно. Можете например да използвате факта, че

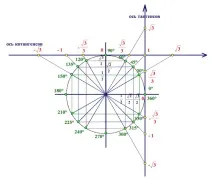
Всъщност картината говори сама за себе си.

Ако не е много ясно, нека да разгледаме примери:

Пример 1.

Изчисли

Намираме на кръга. Свързваме тази точка с точката (0; 0) с лъч (началото е точката (0; 0)) и гледаме къде този лъч пресича допирателната ос. Виждаме това

Отговор:

Пример 2.

Изчисли

Намираме на кръга. Свързваме точката (0;0) с посочената точка с лъч. И виждаме, че лъчът никога няма да пресече допирателната ос.

не съществува.

Отговор: не съществува

Пример 3.

Изчисли

Намираме точка на кръга (това е същата точка като) и от нея по часовниковата стрелка (знак минус!) Отлагаме (). Докъде ще стигнем? Ще се окажем в точката, която имаме на окръжността (виж Фиг.) е наречена като . Свързваме тази точка с точката (0;0) с лъч. Отидохме до допирателната ос към стойността.

Значи означава

Отговор:

Пример 4.

Изчисли

Следователно от точката (тя ще бъде там) отделяме обратно на часовниковата стрелка.

Отиваме до оста на котангенсите, получаваме това

Отговор:

Пример 5.

Изчисли

Намираме на кръга. Свързваме тази точка с точката (0; 0). Отиваме до оста на котангенсите. Виждаме това

Отговор:

За да не загубите страницата, можете да я запазите при себе си:

---