УРАВНЕНИЯ НА КОЛМОГОРОВ - Студиопедия
При съставянето на система от диференциални уравнения (6) е удобно да се използва обозначена графика на състоянията на системата, където всяка стрелка, водеща от състояние в състояние, има интензитета на потока на Поасон от събития, който прехвърля системата от състояние в . Ако нито стрелката, нито съответният интензитет са поставени върху маркираната графика.
 |
При съставянето на уравненията на Колмогоров според графиката на състоянието е удобно да се въведе понятието „вероятностен поток“. Ще наречем вероятностния поток, който прехвърля системата от състояние в състояние продукт на вероятността на състоянието , от което идва стрелката, по интензитета
потокът от събития, който превежда системата по тази стрелка.
Уравненията на Колмогоров (6) се съставят съгласно следното правило: производната на вероятността за всяко състояние е равна на сумата от вероятностните потоци, които прехвърлят системата в това състояние, минус сумата от всички вероятностни потоци, които извеждат системата от това състояние.
Всички интензитети в уравнение (6) могат да бъдат записани като квадратна матрица:
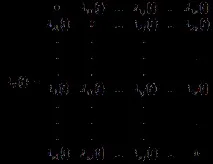
Където . По главния диагонал на тази размерна матрица има нули, а в пресечната точка на i-тия ред и j-тата колона има функция - интензивността на потока на Поасон от събития, които прехвърлят системата S от състояние в състояние.
Матрицата на интензитета (17) може да бъде удобно илюстрирана с помощта на обозначена графика на състоянието на системата S, на която са посочени само тези ръбове между състоянията и за които съответните интензитети не са равни на нула, а съответният интензитет на потока от събития е посочен близо до всеки ръб (фиг. 5). Има едно към едно съответствие между матрицата на интензитета (17) и обозначената графика на състоянията на системата.
Познаване на етикетираната графикасъстояния на системата (или матрицата на интензитета), използвайки мнемоничното правило, може да се напише система от диференциални уравнения за вероятностите на състоянията на системата (6).
Ако всички интензитети на потока не зависят от аргумента t, тогава марковският процес се нарича хомогенен. Ако поне един от интензитетите в матрицата (17) зависи от времето, тогава такъв марковски процес се нарича нехомогенен. За хомогенен марковски процес коефициентите в системата от диференциални уравнения (6) са постоянни.
По този начин, за да изследвате марковски случаен процес, трябва да знаете: 1) матрицата на интензитета (17) (или означената графика на състоянията на системата) и 2) началните условия
, (18)
(19)
Пример. Означената графика на състоянието на системата има формата, показана на фиг. 4.
 |
Напишете уравненията на Колмогоров за вероятностите на състоянието и посочете при какви начални условия те трябва да бъдат решени, ако в началния момент системата S е в състояние с вероятност ½ и в състояние с вероятност ½
Решение. Уравненията на Колмогоров имат формата
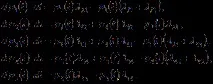
Всяко от тези уравнения може да бъде отхвърлено и вероятността, съответстваща на него, може да бъде изразена по отношение на останалите, като се използва условието за нормализиране:
. (**)
Началните условия, при които ще е необходимо да се реши системата от диференциални уравнения, ще бъдат:
(***)
Уравнения (*) както при постоянен, така и при променлив интензитет (заедно с условието за нормализиране (**)), могат да бъдат решени на компютър при начални условия (***) чрез всеки от изброените методи.
15.QUUE МОДЕЛИ В ИЗЧИСЛИТЕЛНИ СИСТЕМИ И МРЕЖИ. СТРУКТУРА НА СИСТЕМАТА ЗА ОПАШКИ.
За да увеличите натоварването (намалетепрестой) на софтуерни и хардуерни ресурси на изчислителни системи (CS), съвременната организация на изчислителния процес предвижда възможност за създаване на опашки за тях. Пример е опашка от задачи, чакащи за разпределение на паметта, опашка от задачи към централния процесор и за I/O. Задачите, които чакат този или онзи тип услуга (в други случаи това могат да бъдат заявки, съобщения, задачи, процеси или програми), ще се наричат заявки (заявки), а устройството, предназначено за тяхното обслужване (например памет, централен процесор (CPU), входно-изходно устройство) ще се нарича сервизно устройство.
Във VS са възможни опашки, в които приложенията не са задачи в обичайния смисъл на думата. Така например в многопроцесорните компютърни системи по правило само един процесор може да работи с този модул памет (четене-запис) наведнъж. По този начин, ако по време на работа на един от процесорите с определен модул памет възникне заявка от друг процесор към този, тогава той трябва да изчака освобождаването на този модул памет. Ясно е, че в горния пример заявките са заявки от процесора, а обслужващите устройства са блокове памет.
Количественият анализ на опашките в КС изисква отговор на поне два въпроса: колко натоварено е разглежданото обслужващо устройство и какво е времето за изчакване на заявките в опашката? И двата крайни случая, когато сървърът не е достатъчно натоварен, т.е. бездействат дълго време, а когато натоварването е прекомерно голямо, в резултат на което приложенията чакат дълго обслужване, изискват коригиращи решения в управлението на изчислителния процес. Тъй като много ресурси са взаимосвързани във VS, претоварването на един от тях и недостатъчното натоварване на другия може да доведе до намаляване напроизводителност на самолета като цяло.
Методите за решаване на проблемите на количествения анализ на опашките са предмет на един от разделите на теорията на вероятностите, известен като теория на опашките или теория на опашките.
Структурата на системата за масово обслужване
Въпреки че CS е взаимосвързан набор от изчислителни ресурси, в някои случаи основният интерес е задачата за оценка на натоварването на един от тези ресурси, например централен процесор, магнитно дисково устройство или компютърен оператор (например мрежов оператор). Този проблем може да бъде решен в рамките на модели на системи за масово обслужване с едно обслужващо устройство, чиито методи за изследване представляват най-развития и завършен раздел на теорията.
Основните елементи на системата за масово обслужване (QS) са показани на фигурата.
Обслужваната единица в CMO е приложението. Приложенията се изпращат към сервизното устройство. Ако заявките, пристигащи в CMO, не могат да бъдат удовлетворени веднага, тогава възниква опашка. Опашката не е присъща на никое QS. Има такива QS, които опашката не е разрешена и заявката, която установи, че сервизното устройство е заето, се губи. Ако сервизното устройство е заето в момента на получаване на заявката, тогава заявката заема опашка към него, където чака началото на услугата.
Изборът на заявка за услуга в даден момент се прави в съответствие с определено правило, което се нарича дисциплина на услугата. След това приложението се обслужва и след като услугата приключи, приложението напуска системата. Изходящият поток от обслужвани заявки може да бъде много важен в случаите, когато е входящ за друг QS. Например, програмите могаталтернативно изискват поддръжка на CPU и I/O процесора.
Могат да се направят различни предположения относно елементи на QS като входящия поток от заявки, механизма на обслужване и дисциплината на обслужване. Нека се спрем на някои от тях.
Не намерихте това, което търсихте? Използвайте търсачката: