Урок - Призма
Кратко описание на документа:
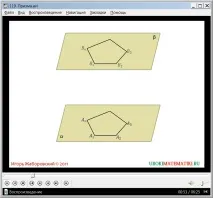
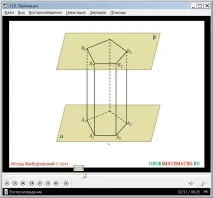
Видео урокът започва с представяне на неговото заглавие. Демонстрацията започва с описание на това как се изгражда призма. Екранът показва две равнини α и β, които са успоредни една на друга. Върху α е очертан многоъгълник А1А2…An. В този случай върху равнината β се очертава многоъгълник В1…Вn, равен на построения върху α. На фигурата, за по-голяма яснота, петоъгълниците са показани в равнините α и β.
Отбелязва се също, че при очертаване на равен триъгълник в равнината β трябва да е изпълнено условието всички страни на построените многоъгълници да са по двойки успоредни. Разкрива се понятието успоредни прави в пространството. Това означава, че в пространството дадените прави лежат в една равнина и не се пресичат. За да могат учениците да представят този факт, фигурата допълнително изобразява равнина, която съдържа съответните страни на многоъгълниците AnA1 и BnB1, изобразени в α и β. Правите, съдържащи дадените страни, не се пресичат, така че те са успоредни една на друга и страните са успоредни. Ако условието за успоредност на страните е изпълнено, се чертаят отсечки, свързващи съответните върхове на многоъгълниците A1B1, ..., AnBn. Тези линии, които не се виждат, са маркирани с пунктирана линия. Така при конструирането получихме n успоредника, които съставляват страничната повърхност на призмата - A1A2B2B1 и т.н. Отбелязва се, че признак, че тези страни са успоредници, е успоредността на съответните страни на многоъгълниците, построени в равнините α и β, както и тяхната равнина. Според конструкцията дефиницията на n-ъгълна призма се извежда като многостен А1А2…AnВ1В2…Вn, образуван от многоъгълници В1В2…Вn и А1А2…An. При коетое посочено, че дадените многоъгълници, образуващи призма, се наричат нейни основи. В допълнение към тези многоъгълници призмата включва гореописаните успоредници A1A2B2B1 и т.н., образувани от страните на многоъгълниците и сегментите, начертани между тях. Паралелограмни данни върху повърхността на призма - странични стени. А сегментите, свързващи върховете на разглежданите многоъгълници, се наричат странични ръбове.
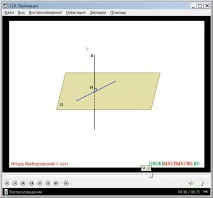
След това се разглеждат видовете призма в зависимост от ъглите, които нейните странични лица образуват с основата. За да се разгледат видовете призми, се въвежда концепцията за перпендикулярност на права линия и равнина. Съответните конструкции са показани на фигурата. За целта са построени равнина α и права a, минаваща през нея. Посочва се, че правата a ще се счита за перпендикулярна на равнината α, ако е перпендикулярна на всяка права, принадлежаща на дадената равнина и минаваща през пресечната точка на тази равнина и правата a. Фигурата показва набор от прави, на които правата a е перпендикулярна. Също така се казва, че ще има безкраен брой такива линии. Въвежда се обозначението за перпендикулярност на права равнина a α и се формулира математически правилно описание на този факт.
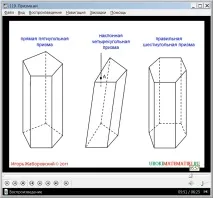
Съобщава се, че права призма ще се нарича, ако всеки страничен ръб е перпендикулярен на основите. Като пример фигурата показва петоъгълна права призма. Отбелязва се, че тази призма се счита за права, тъй като нейните ръбове са перпендикулярни на основите. Той също така определя наклонена призма с ръбове, които не са перпендикулярни на равнините на основите. Даден е пример за наклонена четириъгълна призма. Дадено е определение за правилна призма. Примерът показва правилнотошестоъгълна призма.
Елементите на призмата са описани по-нататък. Посочва се, че ако във всяка точка на основата се начертае права линия, перпендикулярна на тази основа, тогава сегментът, свързващ точките на пресичане на основите с този перпендикуляр, ще се нарича височина на изследваната призма. В четириъгълна призма на фигурата например е показана височината AB. Отбелязва се също, че могат да бъдат построени безкраен брой такива височини, но всички построени височини на призмата са равни и успоредни. Това твърдение ще бъде доказано при изучаване на стереометрия в гимназията.