Векторни модели - Studiopedia
Векторните структури от данни предоставят представяне на географското пространство по по-интуитивен начин и очевидно повече напомнят на добре познатите хартиени карти.
Има няколко начина за комбиниране на векторни структури от данни във векторен модел на данни, който ви позволява да изследвате връзките между индикатори в рамките на едно и също покритие или между различни покрития.
Например спагети моделът, топологичният модел и кодирането на векторни вериги. Най-простата векторна структура от данни еспагети моделът, показан на Фигура 4, който по същество преобразува графично изображение на карта едно към едно.
Тя е представена като най-естествена или най-логична, главно защото картата е реализирана като ментален модел.
Въпреки че заглавието звучи малко странно, то всъщност е доста точно по същество. Ако си представите покриването на всеки графичен обект от нашата хартиена карта с парче (едно или повече) паста, тогава ще получите доста точна картина за това как работи този модел. Всяко парче действа като един примитив: много къси за точки, по-дълги за линейни сегменти, набори от сегменти, свързани в краищата си за граници на региони. Всеки примитив е един логически запис в компютъра, написан като низове с променлива дължина от координатни двойки (X,Y).
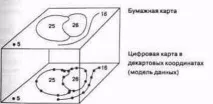
Фиг. 4Спагети модел с векторни данни.
В този модел съседните зони трябва да имат различни спагети вериги за общите страни. Тоест, няма области, за които която и да е спагети верига да е обичайна. Всяка страна на всяка област има свой собствен уникален набор от линии и координатни двойки. Въпреки че, разбира се, общите страни на регионите, дори когато са написаниотделно трябва да имат едни и същи набори от координати. За разлика от спагети моделите,топологичните модели, както подсказва името, съдържат топологична информация в ясна форма. За да се поддържат усъвършенствани аналитични методи, трябва да се включи възможно най-много ясна топологична информация. Точно както математическият копроцесор интегрира много специализирани математически операции, така и топологичният модел на данни интегрира решения на някои от най-често използваните функции в географския анализ. Това се постига чрез включване на информация за съседство в структурата на данните, за да се елиминира необходимостта да се дефинира в много операции. Топологичната информация се описва от набор от възли и дъги. Възелът е повече от просто точка, той обикновено е пресечната точка на две или повече дъги и неговият номер се използва за обозначаване на всяка дъга, към която принадлежи. Всяка дъга (дъга) започва и завършва или в точката на пресичане с друг балон, или във възел, който не принадлежи на други дъги. Дъгите се образуват от последователности от сегменти, свързани с междинни (оформящи) точки.
В този случай всяка линия има два набора от числа: двойки координати на междинни точки и номера на възли. Освен това всяка дъга има свой собствен идентификационен номер, който се използва, за да посочи кои възли представляват нейното начало и край. Регионите, ограничени от дъги, също имат идентифициращи кодове, които се използват за определяне на връзката им с дъгите. Освен това всяка дъга съдържа ясна информация за номерата на областите отляво и отдясно, което ви позволява да намерите съседни области.
Тази функция на този модел позволява на ГИС да знае действителните връзки между характеристиките. По този начин имаме векторен модел на данни, който по-добре отразява каквокак картографираме потребителите дефинират пространствени връзки, записани в традиционен документ.
Не намерихте това, което търсихте? Използвайте търсачката: