Видове секции от двуклонови стелажи

Основни данни за задача № 8

Видове закрепване на пръти

Задача номер 9. Дефиниция на секторен

Характеристики на тънкостенни пръти

За даден тип напречно сечение на тънкостенен прът се изисква следното:

1) определяне на позицията на центъра на тежестта на секцията;

2) начертайте линейни координатиzиy;

3) според построените диаграми изчислете стойността на аксиалните инерционни моменти на сечениетоIzсиI yс;

4) конструиране на диаграма на секторните координатиw;

5) чрез умножаване на диаграмитеzиyпо диаграматаw, изчислете секторно-линейните статични моменти на сечениетоSwzиSwyи определете координатите на центъра на огъване;

6) нанасяне на основните секторни координатиwо;

7) използвайки графикатаwо, изчислете основния секторен инерционен момент на сечениетоIwo;

8) изчислете инерционния момент на секцията с чисто усукванеIt.

Видовете напречно сечение на гредата са показани на фиг. 8. Първоначалните данни за размерите на секцията трябва да бъдат взети от табл. единадесет.

Преди решаването на този проблем е необходимо да се проучи материалът, представен в [1], [2], [11].

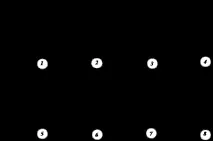
Основни данни за задача № 9

Задача номер 10. Изчисляване на плочата по метода на Риц

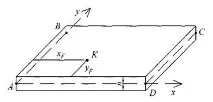
За правоъгълна плоча, натоварена с равномерно разпределен товар с интензитетqи концентрирана силаF, разположена в точкаKс координатиxF,yFс даден израз на функцията на деформация, се изисква:

1) установете условията за поддържане на плочата;

2) използване на метода на Ritz за определяне на коефициентаC;

3) построява диаграми на деформация за посочените сечения на плочите;

4) конструирайте диаграми на огъванемоменти, срязващи сили, въртящи моменти;

5) изградете диаграми на нормални и срязващи напрежения за посочените секции.

Изчислителната схема на плочата е показана на фиг. 9.

От табл. 12, се изисква да се избере функция на отклонение, която да удовлетворява граничните условия по ръбовете на плочата, т.е.

къдетоiе номерът на функцията по посока на остах;j– номер на функция по посока на остаy.

.

Цилиндрична коравина.

Диаграми на вътрешни сили за изграждане по формулите:

;

;

;

;

.

Изградете диаграми въз основа на факта, че в даден участък от плочата нейната дължина и ширина са разделени на четири части.

Диаграмите на напрежението в дадена точка на плочата по нейната дебелина се изчертават по формулите:

;

;

,

където z е разстоянието през дебелината на плочата от нейната неутрална равнина до точката, където се определя напрежението.

Първоначалните данни за изчислението трябва да се вземат съгласно табл. 13.

Функции за отклонение

Основни данни за задача № 10

Задача номер 11. Изчисляване на греда върху твърдо тяло

Еластична основа

За греда, лежаща върху здрава еластична основа, е необходимо да се определят вътрешните сили и премествания, като се използват съответните уравнения на метода на началните параметри.

Работата се извършва на два етапа. На първия етап е необходимо да се запишат уравненията на деформациите и вътрешните сили за всяко сечение на гредата.

Състоянието на напрежение и деформация на греда, лежаща върху здрава еластична основа, зависи от характеристиките на коравината на гредата и еластичната основа. Тези характеристики са:

EJz– коравина на огъване на гредата;

- коефициент на твърдост,

къдетоEе модулът на еластичностматериал на гредата, kN/m 2 ;Jz– инерционен момент на напречното сечение на гредата, m 4 ;K0 е коефициентът на податливост на еластичната основа, в зависимост от свойствата на почвата, kN/m 3 ;b– ширина на напречното сечение на гредата, m.

Когато се изчислява по метода на началните параметри, началото на координатите се избира в най-лявата точка на лъча. Тъй като реакцията на еластичната основа се променя непрекъснато по дължината на гредата, за да се конструират криволинейни диаграми на деформации и вътрешни сили, е необходимо да се определят техните стойности за няколко точки по дължината.

Началните параметри зависят от граничните условия. В табл. 14 са показани уравненията в зависимост от действащите външни натоварвания. В тези уравненияy0,j0,M0,Q0 са началните параметри, два от които винаги са равни на нула (Таблица 15). Неизвестните начални параметри се определят от условията за фиксиране на десния ръб на гредата.

Уравнениятаy,j,M,Q(Таблица 14) включват функциитеY1(x),Y2(x),Y3(x),Y4(x), чиито стойности се определят в зависимост отbxаргумент, къдетоxса координатите на точките на лъча в приетата координатна система:

В зависимост от естеството на действащите натоварвания и от условията на фиксиране на левия край на гредата за всяко сечение е необходимо да се запише уравнението във формата, показана в табл. 14.

Тъй като при съставяне на уравнения за различни секции, всеки път, когато част от гредата се разглежда отляво на сечението, тогава уравнението за всяка следваща секция включва всички членове на уравненията в предишните секции. Следователно записът на уравненията за всеки раздел може да бъде представен под формата на таблица. 16.

---