Въпроси

1. Защо и как външното натоварване се прехвърля към възлите?

2. Как се извършва преходът към обща координатна система?

3. Как се формира глобалната матрица на коравина?

4. Как се вземат предвид граничните условия?

5. Как се изчисляват преместванията и вътрешните сили?

6. Какви са функциите на препроцесора, процесора и постпроцесора?

7. От какви стъпки се състои алгоритъмът FEM?

Лекция 16 Динамика на структурата

1. Въведение в динамиката на конструкцията

Трептенията представляват една от най-често срещаните форми на движение. Клоните на дърветата се люлеят, металната плоча, захваната в менгеме, люлките, количките на пружини се движат, водата и предметите върху нея се люлеят. Сградите и конструкциите се люлеят от вятър, земетресения, от работата на различни машини и механизми. Когато конструкцията вибрира, величините и знаците на вътрешните сили (напрежения) се променят непрекъснато, което може да доведе до бързо разрушаване на отделни елементи, части или цялата конструкция.

Динамиката на конструкциитеизучава механичните вибрации на конструкциите. Като теоретична наука, тя разработва различни методи и алгоритми за изчисляване на конструкции за динамични ефекти. В същото време тя е приложна наука и решава конкретни проблеми. Сред задачите, решавани от динамиката на конструкциите, най-важни сачетири задачи на динамиката:

1) определяне на честотите и режимите на собствените трептения;

2) проверка за резонанс;

3) проверка на динамична якост;

4) проверка на динамичната твърдост.

Решаването на задачи на динамиката е много по-трудно от решаването на задачи на статиката, т.к Друг фактор, който трябва да имате предвид, е времето.

При изчисляване на вибрациите се взема предвид структуратакатоосцилираща система. Осцилаторните системи са разделени на два вида.Дисипативна системае система, в която енергията се разсейва (разсейва).Консервативна системае система, в която разсейването на енергия се пренебрегва.

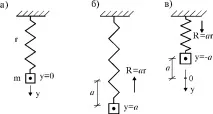
Най-простият модел на консервативна трептителна система е система от пружина и една маса (фиг. 16.1 а). Коравината на пружинатаrхарактеризира еластичността на системата, а масатаmхарактеризира нейните инерционни свойства.

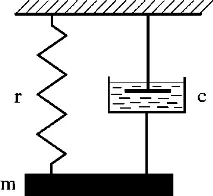
Най-простият модел на дисипативна система е система от пружина, вискозен елемент и маса (фиг. 16.2). Съпротивителната силаc, възникваща във вискозния елемент, се стреми да спре трептенията на системата. Такъв елемент се наричаамортисьор(илиамортисьор). Следователно, дисипативната система често се наричазаглушена система.

Ориз. 16.1 Фиг. 16.2

2. Степен на свобода и изчислителен модел на трептящата система

Степента на свобода в динамиката на конструкциите се разбира като посока на възможното независимо движение на индивидуална маса. За разлика от концепцията за степента на свобода в кинематичния анализ, при определяне на динамичните степени на свобода се вземат предвид и деформациите на елементите.

Броят на динамичните степени на свободаWdynе най-малкият брой параметри, необходими за определяне на позицията на всички маси на системата.

Ако разглеждаме конструкцията като система от безкраен брой елементарни маси, получаваме система с безкраен брой динамични степени на свобода. Изчисляването на трептенията дори на най-простите системи (греди, плочи или черупки) с помощта на такъв континуален модел е трудна задача. Следователно в динамиката на конструкциите изчислителният модел е избран под формата на система сконцентрирани маси.

Масите на една структура могат да бъдат дискретизирани по различни начини. Понякога чрез концентриране на разпределената маса на структурата само в няколко точки е възможно да се изчислят точно най-простите вибрации.

Масата на конструкцията обикновено се концентрира в характерни точки, където действат най-големите натоварвания. Ако положението на такива точки е трудно да се установи, местата и величините на концентрираните маси могат да бъдат намерени от условието за равенство на енергиите на цялата система и нейния дискретен модел. Събраните маси, определени по този начин, се наричат ​​редуцирани маси. Големи маси, концентрирани върху конструкцията (товари, различни машини, машини, оборудване и др.) се считат забукови маси.

Намалените и буци маси на плоска система имат три степени на свобода: те могат да осцилират в две независими взаимно перпендикулярни посоки и да се въртят около центъра на масата. Ако въртенето (торсионните вибрации) на масата не се вземе предвид, получаваметочкова маса. Броят на степените на свобода на точкова маса е две.

Нека разгледаме някои примери.

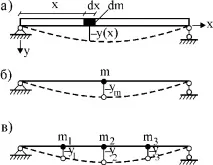
1. Шарнирна греда (фиг. 16.3 а) се състои от безкраен брой елементарни масиdm, чието положение се определя от безкраен брой преместванияy(x). СледователноWdyn=∞. Ако масата на лъча е концентрирана в една точка, положението на масата на точкатаmще се определя от един параметър - преместванетоym(фиг. 16.3 b). ТогаваWdyn=1. Ако масата на лъча е концентрирана в три точки, тогава с

2. Водна кула (фиг. 16.4 a) и едноетажна рамка (фиг. 16.4 c). Основните им маси са разположени на върха. Следователно те могат да се разглеждат като трептящи системи с една маса и една степен на свобода, т.е.вземетеWdyn=1(фиг. 16.4 b, d).

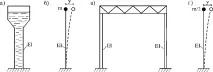
Ориз. 16.3

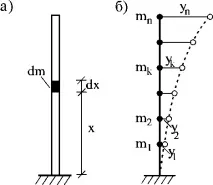
3. Комин с разпределена маса (фиг. 16.5 а) не може да се разглежда като динамична система само с една степен на свобода, тъй като това води до неточни резултати. Тя трябва да се разглежда като система с достатъчно голям брой степени на свобода (фиг. 16.5 b) и да се приемеWdyn=n.

---