Въведение - страница 2

Въведение в теорията на стабилността_________________________________________________ 11

често води) до пълно унищожаване на популацията на нестабилност на равновесното положение x 0 = с 1 = с 2 .

3 около. Видове устойчивост по изходни данни.

1) Стабилност по Ляпунов.

Този тип стабилност реализира идеята за близостта на интегралните криви за 0 ≤ t ∞. За скаларното уравнение x & = f(t, x) на примера на решението x =

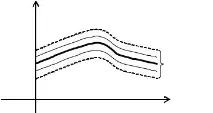
x(t; 0 ,x 0 ) с начални данни (0, x 0 ) (виж фиг. 7) Стабилността на Ляпунов може да се характеризира, както следва:

( ε > 0 ) ( δ *> 0) ( δ (0 , δ * )) ( t ≥ 0 ) : x = x(t; 0 ,x 0 ± δ )

Както можете да видите, стабилността на Ляпунов означава, че чрез избиране на началото на смутитата интегрална крива в момента t = 0 достатъчно близо до точката x 0 на непроблемната (удебелена) интегрална крива, е възможно да се гарантира, че смутената интегрална крива не напуска границите на произволно тясна непроблемна интегрална крива с неограничено увеличение във времето.

Ориз. 7. Стабилност по Ляпунов.

2) Стабилност на Поанкаре (орбитална стабилност).

Тук също се прилага идеята за близост, но не за интегрални криви, а за траектории, т.е. проекции на интегрални криви върху фазовото пространство.

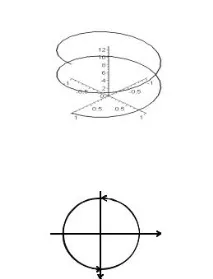
Например, спирална крива, дефинирана в пространството от уравненията x = sint, y = цена, t ≥ 0 (фиг. 8),

Въведение в теорията на стабилността_________________________________________________ 12

---