Забележки относно стелациите и съвпадите на Платоновите тела

Терминът "звезда" има общ корен с думата "звезда" и това показва неговия произход. Имазвездни многоъгълнициизвездни многостени. За да разберем същността на въпроса, се обръщаме към чертежите и моделите.

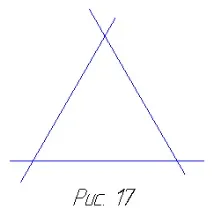
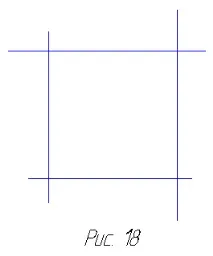
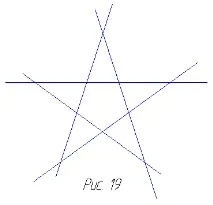
Нека започнем с най-простия многоъгълник - равностранен триъгълник. Нека да видим какво ще се случи, ако продължим и трите му страни. Лесно е да се види, че нито една нова част от равнината няма да бъде ограничена от тези линии: разширенията на страните ще се разминават (фиг. 17). Подобна картина ще се появи пред нас, ако се опитаме да продължим страните на квадрата. Построените прави ще бъдат по двойки успоредни и няма да се пресичат, колкото и да са продължени (фиг. 18). Така те няма да добавят нови ограничени части от равнината към вътрешността на квадрата. В случай на петоъгълник обаче картината се променя. Продълженията на страните на петоъгълника се пресичат във външната част на равнината по отношение на петоъгълника, добавяйки нови части към петоъгълника. Резултатът е добре позната петлъчева звезда, иначе наричанапентаграма(фиг. 19). Пентаграмата е била известна още в

древни времена, което става ясно от факта, че питагорейците са я смятали за символ на здравето. Продължаването на страните на шестоъгълника води до появата на шестоъгълна звезда илихексаграма(последната може да се разглежда не като един многоъгълник, а като връзка на два равностранни триъгълника).

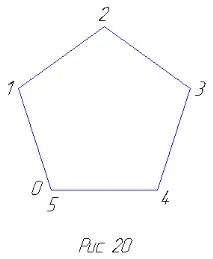
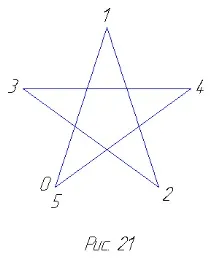
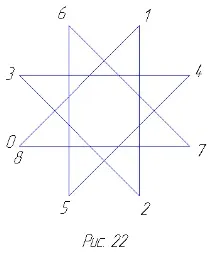
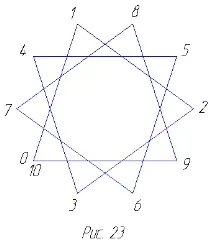
По същия начин, правилен осмоъгълник (октагон) ни води до осмоъгълна звезда -октаграма, правилен десетоъгълник (декагон) - до десетоъгълна звезда илидекаграм. Пентаграма, октаграма и декаграма могат да бъдатсе разглеждат като неразпадащи се равномерни многоъгълници със съответно 5, 8 и 10 страни, тъй като има непрекъснато обхождане на техните върхове по страните около центровете. Освен това, в случай на пентаграма, например, правейки пълна верига в реда, определен от числата 0-5 (фиг. 21), ние правим две завъртания около центъра на пентаграмата, докато при обикаляне около петоъгълника (фиг. 20) правим само едно завъртане. При октаграма и декаграма се получават три

оборота около центъра (фиг. 22 и 23). Обърнете внимание, че ние не считаме вътрешните пресечни точки за звездни върхове. Горното обстоятелство се взема предвид при символното означение на звездовидни многоъгълници. В нашия случай пентаграмата, октаграмата и декаграмата се означават съответно с 5/2, 8/3 и 10/3. Тези звезди могат да приемат и други форми,

но в бъдеще ще говорим само за формите, описани по-горе ([4], стр. 63 и сл.).

Ако сега се обърнем към подобен процес в триизмерното пространство, тогава е естествено да започнем отново с най-простия многостен - тетраедъра. Разбира се, тук трябва да продължим не ръбовете, а лицата на полиедъра. Четири равнини обаче - продължения на лицата на тетраедъра - ограничават само тази част от триизмерното пространство, която съвпада с първоначалното тяло. Шестте равнини на куб са по двойки успоредни и взаимно перпендикулярни, като страните на двуизмерен аналог на куб, квадрат. Следователно в триизмерния случай не се добавят нови части към куба. Но вече случаят с октаедър дава интересни резултати. Осем равнини - продължения на лицата на октаедъра -

отделят нови части от пространството, така да се каже, "отделения", външни за октаедъра. Ще откриете, че тези части не са нищо друго освен малки тетраедри, чиито основи съвпадатлицата на октаедъра. Ако сега мислено прикрепите тези части към октаедъра по такъв начин, че техните общи лица с октаедъра да изчезнат, оставяйки вътрешността на новото тяло куха, пред очите ви ще се появи неизпъкнал многостен.

Можете обаче също толкова добре да си представите този полиедър като набор от пресичащи се триъгълни лица, чиито върхове съвпадат с върховете на малки тетраедри. Тези триъгълни лица имат свойството, отбелязано за изпъкналите полиедри, а именно, че всеки ръб на тези триъгълници принадлежи точно на две такива лица: Разбира се, тези ръбове се пресичат, но вътрешните точки на пресичане на тези сегменти не трябва да се разглеждат като върхове на многостена, както направихме в случая на плоски звездни полиедри. В края на краищата, дори и там всяка страна, например, пентаграми, пресечени от две други, но точките на тяхното пресичане не се считат за разделяне на страната. По същия начин в звездовиден октаедър намираме само осем лица и само краищата на ръбовете се считат за върхове на полиедъра.

По-нататъшното внимателно изследване обаче ни води до идеята, че този полиедър всъщност не е едно тяло, а комбинация от два пресичащи се тетраедъра, чиито центрове съвпадат с центъра на оригиналния октаедър и тази точка е центърът на симетрия на цялото тяло. Този полиедър е открит от Кеплер през 1619 г. и е нареченстела октангула1

Друга особеност на това тяло е, че осемте му върха лежат на върховете на определен куб, а ръбовете са диагоналите на лицата на този куб.

Няма смисъл да продължаваме отвъд лицата на октаедъра, защото те вече няма да отделят никоя част от пространството, няма да създават нови „отделения“. Следователно октаедърът има само една форма на звезда.

Акообърнете се към додекаедъра, разширявайки лицата му, както в случая с октаедъра, ще откриете, че това ще доведе до образуването на три различни типа отделения. В близост до самия додекаедър има 12 петоъгълни пирамиди. Тези пирамиди превръщат додекаедъра вмалък звездовиден додекаедър. Те са последвани от 30 отделения с клиновидна форма, превръщащи малкия звездовиден додекаедър вголям додекаедър. И накрая, 20 триъгълни бипирамиди 2 превръщат големия додекаедър ввелик звездовиден додекаедър, който може би би бил по-точно нареченвелик звездовиден додекаедър. Това е последната звезда на додекаедъра, която има три такива форми: две от тях са открити от Кеплер (1619), третата от Поансо (1809).

Сега може да се заинтересувате от факта, че за разлика от октаедъра, никоя от звездите на додекаедъра не е съединение на Платоновите тела, а образува нов полиедър. Всъщност тези полиедри са правилни, тъй като два от тях имат лица от 12 пресичащи се пентаграми, а лицата на третия имат 12 пресичащи се петоъгълници (петоъгълници). Коши (1811) доказва, че тези три открити по-рано полиедъра всъщност не са нищо друго освен звездовидни образувания на додекаедъра [24]. Той също така установи, че заедно с големия икосаедър - звездовата форма на икосаедъра - те са единствените възможни правилни звездовидни тела. И така, към петте правилни тела, известни на древните учени, математиците от по-близка епоха добавиха четири звездовидни полиедра, лицата на които могат да бъдат правилни или звездообразни многоъгълници. Както и преди, лицата са свързани по двойки в краищата, но преди това се пресичат с други лица. В този случай вътрешните пресечни линии не се считат за ръбове. Всички тези свойства се виждат ясно на моделите.звездовидни тела.

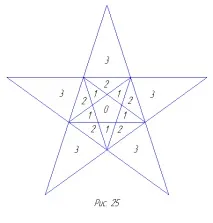
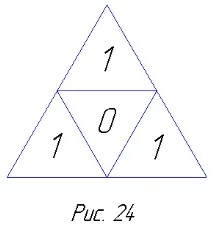
Преди изграждането на тези модели е интересно да се запознаете със структурата на шаблоните, които определят всяко едно лице на предна звезда. Останалите лица имат подобна структура. Шаблонът за октаедъра ще бъде равностранен триъгълник, от който трябва да се изреже триъгълник с върхове в средните точки на страните (фиг. 24). Този вътрешен триъгълник е лицето на оригиналния октаедър, извън който е разположенастела октангула. Шаблонът за додекаедъра е звездовиден многоъгълник без изрязан звездовиден многоъгълник (фиг. 25). Номерирането показва кои части образуват частите, външни за лицата. С помощта на такива шаблони можете да направите заготовките, необходими за производството на модели.

На следващите страници светло засенчване показва онези части от лицата, които се виждат от съответните върхове на многостена, разположен над разглежданото лице. Черният цвят показва част от същото звездно лице, видимо от противоположната страна. За всички избрани части имаме възможност да преценим какви да бъдат заготовките за даден модел.

1Stella octangula(лат.) - осмоъгълна звезда. 2Бипирамидае многостен, образуван от двеn-въглищни пирамиди, които са сгънати с еднакви основи (и са разположени на противоположните страни на общата основа).