5.3.2. логаритмично разпределение
Разпределението на честотата на вида за логаритмично разпределение се описва със следната последователност:
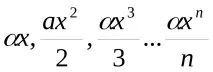
където хе броят на видовете, представени от един индивид, х 2/2 е броят на видовете, представени от два индивида и т.н.
Логаритмичният модел има два параметъра иx. Това означава, че за проба с размерNи брой видовеS, има само едно възможно разпределение на честотите на видовете според тяхното относително изобилие, тъй като и , иxса функции наNиS. Колкото по-голяма е извадката, взета от дадена общност, толкова по-голяма е стойносттаxи толкова по-малък е делът на индивидите, принадлежащи към вида, представен от един индивид в извадката. Два параметъраSиN(общ брой индивиди) са свързани помежду си чрез зависимост, където е индексът на разнообразие, който може да се получи от уравнението:
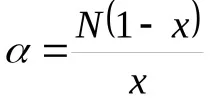
където сумата от всички индивидиN, принадлежащи къмSвидове:
.
Логаритмичен модел на разпределение, характеризиращ се с малък брой разпространени видове и голяма част от "редки" видове, е най-вероятно да опише съобщества, чиято структура се определя от един или няколко екологични фактора.
Както показват проучванията, проведени от Magarran в Ирландия (1992), тази серия съответства на разпределението на изобилието от видове сухоземни растения в иглолистни култури при условия на слаба светлина.
5.3.3. лог-нормално разпределение
Повечето общности проявяват логаритмично нормално разпределение на изобилието на видовете, но този модел обикновено показва голяма, зряла и разнообразна общност. Такова разпределение е типично за системи, в които стойността на дадена променлива се определя от голям брой фактори.
Този модел е приложен за първи път в дистрибуциятаизобилие от видове Престън. На различни емпирични материали той показа, че честотите на видовете в големи проби се разпределят в съответствие с логаритмично нормалния закон. Според разработения от него метод видовете с брой индивиди, затворени в интервали, които са ограничени от числата на геометрична прогресия, се групират в честотни класове. Престън начерта изобилието на видовете по логаритмична скала с основа 2 (log 2) и нарече получените класове октави. Но всяка основа на логаритъма може да се използва за описание на модела. На получената по този начин графика на разпределението на честотите на видовете по класовете на изобилие те съответстват на известната крива на нормалното разпределение, пресечена отляво, в областта на честотите на редки видове.
Разпределението обикновено се записва във формата:
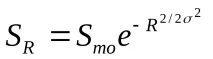
SR– теоретичен брой видове в октава, разположени в R октави от модалната октава;Smo– брой изгледи в модалната октава;– стандартно отклонение на теоретичната логаритмично нормална крива, изразено в брой октави.

Фиг. 5.3.2. Лог-нормално разпределение
Логаритмично нормалното разпределение се описва със симетрична "нормална", т.е. камбанообразна крива (фиг. 5.3.2.). Въпреки това, ако данните, на които съответства, са от ограничена извадка, тогава лявата страна на кривата (т.е. редките, неотчетени видове) ще бъде неясна. Престън нарече тази точка на отрязване на кривата вляво "линия на завесата". Линията на завесата може да се измести наляво с увеличаване на размера на пробата. На фигурата е обозначено със стрелка. За повечето проби се изразява само частта от кривата вдясно от режима. Само с огромно количество данни, събрани в обширни биогеографски области, може да се проследи пълна крива.S-образна крива показва комплексприродата на диференциацията и припокриването на нишите. Повечето видове в естествени отворени екосистеми съществуват в условия на конкуренция за ресурси, а не в условия на пряка конкуренция; много адаптации правят възможно разделянето на ниши без конкурентно изключване от местообитанието. Този модел най-вероятно е за необезпокоявани общности.