6.3. Абсорбиращи вериги на Марков
Това е името на процесите в системата, чиито всички състояния са или поглъщащи, или необратими.
Нека направим промени в матрицатаQот предишния параграф. Променяйки номерирането на състоянията на системата, ние й даваме следния вид

Характерно за тази форма на матрицата е, че първо се посочват поглъщащите състояния (в случая едното), а след това невръщащите се. Такава структура на матрицата на вероятностите за преход се нарича канонична. Може да му се даде следната блокова структура.
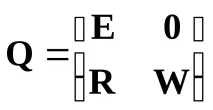
ТукEе подматрицата на идентичност, чийто ред съвпада с броя на абсорбиращите състояния;W- квадратна подматрица на вероятностите за преход върху множеството от състояния без връщане;R- правоъгълна подматрица на преходите от невръщащи се към поглъщащи състояния;0- нулева подматрица. Ако общият брой на състоянията еm, от коитоnса неотменими иl=m-nпоглъщащи, тогава подматрицата има следния ред:
Използвайки уравненията на Колмогоров-Чапман (6.2), получаваме матрицата на вероятностите за преход вkстъпки
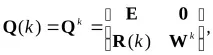
Където
Елементът на подматрицата е вероятността за преход от първоначалното невръщащо се състояние към абсорбиращото състояние вkстъпки. Подматрицата характеризира преходите на системата върху множеството от невъзвратни състояния. Елементите на тази подматрица клонят към нула с увеличаване на броя на стъпките.
Средният брой попадения на системата във всяко отnневръщащи се състояния, ако първоначалното състояние е , се съдържа в матрицата
Тази матрица се нарича фундаментална.
Използването на основната матрица ви позволява да решавате различни проблеми. Например, общият брой стъпки до абсорбция за различни начални състояния е
където1е колонен вектор,съставен от единици.
Вероятността за поглъщане в състоянието, ако първоначалното състояние еsiсе дава от матрицата
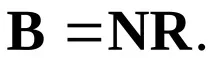
6.4 Ергодични вериги на Марков
Това е името на процесите в системата, всички състояния на която са ергодични. В противен случай системата може да премине към всяко от тези състояния в краен брой стъпки. Разбира се, в този случай няма абсорбиращи и необратими състояния.
Ето най-простият пример за ергодична верига от текстологията, наука, намерила приложение в автоматизираните системи за машинен превод. Българският има 32 букви, от които 9 са гласни. Следователно вероятността за поява на гласна 9:32 на дадено място в текста = 0,28. Това е средно. Всъщност тази вероятност зависи от това дали предишната буква е била гласна (G) или съгласна (S). Ако обозначимq11 като вероятност гласна да се появи след гласна иq22 като съгласна след съгласна, тогава матрицата на вероятността за преход ще приеме формата
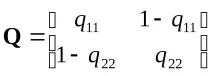
Така моделът за редуване на букви в текст е проста хомогенна ергодична верига на Марков.
Друг пример е заимстван от теорията за оптимизиране на параметрите на системи и процеси чрез произволно търсене. Некаq11 е вероятността за успешен опит за промяна на системните параметри след успешен, аq22 е вероятността за неуспешен опит след неуспешен. В случай на успех системните параметри се променят, в случай на неуспех параметрите остават същите. Съответната графика на състоянието е показана на фиг. 6.4.
Ако матрицата на вероятностите за преход на такава верига е хомогенна, тогава в системата се установява стационарен процес във времето; това означава, че вероятностите за състоянията на системата остават постоянни:
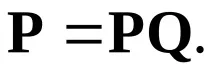
Тези вероятности се наричат окончателни. От (6.3) следва, че
защото,в противен случай, матрицата на вероятностите за преход вkстъпки не зависи отk, ако, разбира се,kе достатъчно голямо.