Алгоритми за събиране и предварителна обработка на измервателна информация
1. Типични алгоритми за събиране на измервателна информация
2. Въвеждане на изменения
3. Изглаждане на оригиналните данни
Темата на теста "Алгоритми за събиране и предварителна обработка на измервателна информация" по дисциплината "Измервателни информационни системи (IMS)".
Софтуерът и математическият софтуер на IMS са не по-малко важен компонент от хардуера. Алгоритмите за събиране и обработка на информация до голяма степен се определят от естеството на задачите, които се решават, и следващите глави ще бъдат посветени на този въпрос. Съществуват обаче редица алгоритми, които могат да бъдат общи за различни IMS.
1. Типични алгоритми за събиране на измервателна информация
Неразделна част от алгоритмите за събиране на първична измервателна информация е нейната дискретизация.
Срещаме дискретност при събиране на първоначална информация и при нейната обработка. На определен етап от развитието на IMS дискретизацията и на двата етапа доведе до грешки в резултатите от измерванията. С ограничената компютърна технология от този период грешката в изчислението беше сравнима с хардуерните и методологичните грешки. Възможностите на съвременните компютри обаче са такива, че грешката, която причиняват в процеса на дискретизация, няма практическо значение. Капацитетът на числата в компютъра винаги е много по-голям от капацитета на входната информация. Изчисляването, например, на интеграли на аналитично дадени функции се свежда до изчисляване на суми от дискретни стойности на тези функции. В този случай винаги може да се осигури необходимата точност на изчисленията. Значително по-голямо влияние има дискретизацията, свързана с алгоритъма за събиране на изходна информация и поради естеството на ИО.
Физическите величини, чиито кодове се издават от измервателния канал, неизбежно се подлагат на дискретизация по нива. Поради ограничеността на броя на битовете на ADC (n), дискретността на физическата величина x, възприемана от канала, е равна на
където X е обхватът на възможните промени в x.
Характеристиката на АЦП с правилно закръгляване е показана на фиг. 1.
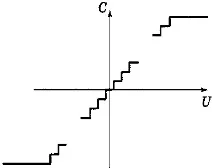
При закръгляване надолу (цялата част от непълния дискрет се изхвърля) характеристиката се измества с bx/2 надясно, при закръгляване нагоре, със същото количество наляво.
Дискретизацията на нивото води до грешка, която има равномерно разпределение в интервал с дължина bx. Стандартното отклонение на тази грешка е a = bx/2 √3, а математическото очакване е нула, когато е закръглено правилно в ADC, -bx/2, когато е закръглено надолу и bx/2, когато е закръглено нагоре. От казаното следва, че имаме доста просто универсално описание на грешките на дискретизация по ниво.
Важна характеристика на грешката на дискретизацията е независимостта на нейните стойности за различни резултати. Това свойство се използва широко при моделиране на произволни равномерно разпределени числа. Благодарение на това свойство, с осредняване и други алгоритми за обработка, които водят до компресиране на резултатите, влиянието на тази грешка е значително намалено и разпределението на грешката на резултата от обработката може да се счита за близко до нормалното.
При малък брой ADC битове грешката на дискретизацията може да бъде значителна и трябва да се вземе предвид при оценката на надеждността на получените резултати. Разрядният капацитет на ADC в ИС е по-малък от разрядния капацитет на числата в компютъра. Независимо от това, винаги можете да изберете такава битова дълбочина на наличния в търговската мрежа ADC, при която грешката на дискретизация по нивоще бъде пренебрежимо малък.
Дискретизацията на стойностите на аргумента (аргументите) при изследването на функциите има по-значително влияние. Най-често изследваните функции на времето са, когато някои или всички физически величини, свързани с IO, зависят от времето. Аргументите обаче могат да бъдат пространствени координати и всякакви други физически величини. В този случай се сблъскваме със сериозен методически проблем - невъзможността за измерване на функцията като цяло. Можем да измерим краен брой функционални стойности за някакъв набор от стойности на аргументи. По правило съседните стойности на аргументите са отдалечени една от друга на равни интервали - равномерна стъпка на дискретизация (квантуване) в аргумента. Понякога обаче се използва и неравномерна стъпка на вземане на проби.
Нека се съсредоточим върху дискретизацията на времето.
В този случай IC дават стойностите на изследваната физическа величина xj, взети във времеви точки tj . Естествено, тези показания, представени в цифров вид, са квантувани по ниво и в зависимост от скоростта на промяна на изследваното количество, съседните показания могат да се различават едно от друго с няколко отделни стъпки. От това следва, че грешката при реконструкцията на функция от нейните дискретни отчети може да бъде много значителна и зависи не само от интервалите от време между съседни показания, но и от скоростта на промяна на изследваната физическа величина. В този случай нямаме същото просто описание на грешката при дискретизация, както при дискретизацията на ниво. Трябва да се отбележи, че задачата за възстановяване на функция от нейните показания не е задължителна при изучаването на функция. Както ще видим в следващата глава, количествата, които ни интересуват, в повечето случаи могат да бъдат определени директно от дискретни показания. Анализ обачегрешките при определянето на тези количества ще бъдат специфични за всяка конкретна задача и ще изискват определена априорна информация за изследваната функция.
Като се има предвид дискретизацията на нивото на дадено количество, ние отбелязахме, че броят на тези нива е почти винаги голям и те са близо едно до друго. При дискретизация във времето моментите на отчитане са доста отдалечени един от друг. Трябва да се има предвид, че tj също са дискретизирани по отношение на нивото. Стъпката на вземане на проби от време може да бъде направена достатъчно малка и винаги е много по-малка от интервалите от време между съседни проби. Тази дискретност обаче също трябва да се вземе предвид. Освен това може да се окаже по-значим, ако аргументът не е времето, а някаква друга стойност.
Грешката поради дискретизацията на аргументите ще бъде толкова по-малка, колкото по-често се вземат пробите. Очевидните физически ограничения на честотата на дискретизация са времето за преобразуване на ADC, пропускателната способност на комуникационните канали и скоростта на компютъра. Тези фактори трябва да се вземат предвид, но те не са решаващи. Инерцията на IO и инерцията на MC, поради инерцията на измервателните преобразуватели, първични и вторични, имат много по-голям ефект.
Ако обектът е достатъчно инерционен и следователно функциите xi (t) са достатъчно бавни (достатъчно нискочестотни), увеличаването на честотата на дискретизация няма да увеличи значително информационното съдържание на първичните данни. Възможно е да се повиши надеждността на тези данни чрез тяхното осредняване, но това увеличение също не е неограничено. Този фактор, който не зависи от свойствата на IMS, ограничава действително необходимата честота на вземане на проби отгоре.
По същия начин не е подходящо да се вземат показания с период, значително по-малък от времеконстантата (времето за запаметяване) на измервателните преобразуватели.Тази ситуация обаче е коренно различна от предишната и означава, че задачите за избор на честота на дискретизация и осигуряване на необходимата скорост на IC трябва да се решават съвместно. Бавността на изследваните функции е отражение на реалните свойства на IO, а тяхното изкривяване поради инерцията на MC и произтичащата от това ниска честота на дискретизация води до увеличаване на хардуерните грешки. Следователно скоростта на МК трябва да бъде съобразена с възможната скорост на изменение на измерените стойности и едва след това може да се избере рационална честота на дискретизация.
Съседните показания на функцията могат да се различават значително едно от друго, но тяхната разлика в абсолютната стойност е средно по-малка от абсолютните стойности на самите показания. Това обстоятелство се използва за компресиране на данни по време на предаването им по цифрови комуникационни канали (разликова модулация). В този случай първата проба се предава изцяло, а в следващите моменти се предават разликите xj - xj -1 , Очевидно такова предаване на информация е по-малко шумоустойчиво от предаването на функционални проби, тъй като повредата в предаването на една разлика не се елиминира при предаване на следните стойности. Въпреки това, поради доста високата устойчивост на шум на цифровите комуникационни канали поради използването на кодове за коригиране на грешки, тази грешка се оказва доста малка. При модулация на разликата стойностите на tj могат да бъдат както еднакви, така и неравномерни.
Разновидност на диференциалната модулация е делта модулацията, която по принцип предполага неравномерно време на вземане на проби. Същността на делта модулацията е, че един бит информация се предава по комуникационния канал в момента, когато измерената стойност се е променила по ниво с една проба. Предаваният бит съдържа информация за знака на промяната (фиг. 2).
В този случай показаниятаще следва толкова по-често, колкото по-голяма е скоростта на промяна на измерената стойност. От тази гледна точка делта модулацията може да се разглежда като адаптивна процедура за събиране и предаване на данни. В този случай разликата между дискретното и непрекъснатото представяне на функцията няма да надвишава един дискретен.
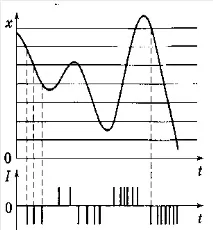
Очевидно предаването на данни с компресиране на информация изисква наличието в IR на изчислителни устройства, които определят разликите и генерират командни сигнали за предаване на данни. По-подробна информация за диференциалната модулация, делта модулацията и други методи за компресиране на данни по време на предаване може да се намери в [29].