Автоматизация на измерванията, контрола и изпитванията
6.3 Измерване на индуктивност, качествен фактор, капацитет и тангенс на загубите
Най-често срещаните променливотокови мостови вериги, измерванията на индуктивността и качествения фактор на бобините са показани на фиг.30. Използват хармонични източници на ток с амплитуда на напрежението U и ъглова честота ω. Тези четирираменни мостове отговарят на най-добрата конвергенция (балансиране). д
Еквивалентните еквивалентни вериги за индуктори със загуби могат да бъдат последователни или паралелни в зависимост от загубите, показани от активното съпротивление.
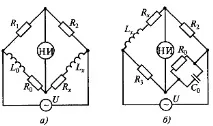 |
Условието за равновесие за веригата на фиг. 30, а има формата
където Lx и Rx са измерените индуктивност и съпротивление на омичните загуби в намотката; LQ и R0 са примерни индуктивности и съпротивления.
Приравнявайки отделно реалните и въображаемите членове на формула (30), получаваме:
LX=L0R2/Ri; RX=R0R2/Rh(31)
Тъй като производството на висококачествени примерни бобини причинява определени трудности, кондензаторът често се използва като примерна мярка в AC мостове (фиг. 30, b). За тази схема
Приравнявайки поотделно реалните и въображаемите части в това уравнение, получаваме следните формули за определяне на параметрите на индуктора:
Lx=C0R2R3; Rx=R2R3/R0.(33)
(34)
За измерване на капацитета и тангенса на ъгъла на загуба на кондензатори с ниски загуби се използва мостова схема, показана на фиг. 31, а (серийно свързване на елементите Cxi Rx), и с големи загуби - на фиг. 31, b (успоредносвързване на елементи Cx и Rx).
Условието за равновесие за веригата на фиг. 31, а има формата
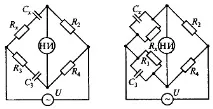
a - с ниски загуби; б - с големи загуби.
Разделяйки тук реалните и въображаемите части, получаваме следните формули за определяне на параметрите на кондензатора:
Cx= C3R4 /R2, Rx=R3R2/R4.(35)
Тангенс на загуба на кондензатор
(36)
За мост с паралелна връзка Cx и Rx (фиг. 31, b) условието за равновесие има формата
(38)
Тангенсът на ъгъла на загуба на кондензатора с паралелна еквивалентна верига:
Тъй като условията за балансиране на моста са зависими от честотата, измервателните схеми на моста са проектирани да работят на една от посочените честоти, например: 50, 100, 1000, 10 000, 100 000 Hz.
Балансиращите вериги се постигат чрез алтернативно регулиране на променливи примерни съпротивления или капацитети. Тази процедура се нарича стъпки и броят на стъпките определя конвергенцията на моста. Мостът с добра конвергенция има не повече от пет стъпала. Балансираните AC мостове осигуряват грешка при измерване от 0,5 до 5%.
6.4 Методи за измерване на резонансна верига
Резонансните методи за измерване използват физични явления в осцилаторни кръгове и генератори. Съответно методите се разделят на контурни и генераторни. Генераторните методи в момента намират ограничено приложение поради различни причини. Най-универсалното устройство за измерване на параметрите на веригата е куметър (от латинската буква Q - характеристики на качествения фактор на индуктор), в който основната измервателна верига е серияколебателна верига.
Опростена блокова схема на kumeter е показана на фиг.32. Източникът на синусоидални сигнали, подавани към последователната резонансна верига, е генератор на ток, натоварен с малко активно съпротивление R0 ≤ 0,05 Ohm. Честотата на изходните трептения на генератора може да варира в широк диапазон. Нивото на входния сигнал трябва да се поддържа постоянно (според VI волтметър).
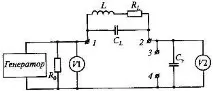 |
При измерване на индуктивност бобината се свързва към клеми 1-2. В този случай резонансната верига ще се формира от бобина с измерена индуктивност Lx с активни загуби RL и междувитковия капацитет на нейните проводници CL, както и регулируем еталонен капацитет Ce. Резонанс във веригата при дадена честота се постига чрез промяна на стойността на капацитета Ce, референтния кондензатор. Резонансното състояние на веригата се определя от волтметър V2, калибриран в стойности Q. Ако капацитетът Ce се измерва при две резонансни честоти, тогава те могат да бъдат изчислени с помощта на следните уравнения:
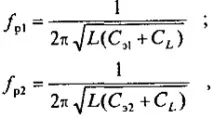 |
където Ce1 и Ce2 са известни еталонни капацитети при резонансни честоти ƒp1 и ƒР2, съответно.
Нека отношението на честотите ƒp1 = KƒР2, където K е коефициент — реално число. Тогава съвместното решение на уравнения (40), (41) дава възможност да се изчислят неизвестните преди това стойности на параметрите L и CL:
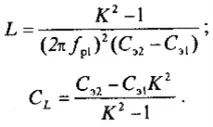
С помощта на измервателния уред можете също да определите неизвестните параметри R, C, tgδc, като свържете измерения резистор или кондензатор към клеми 3-4.