Цифрова обработка на сигнала
цифрова обработка на сигнала
Тема 4. Разликови филтри и интеграционни филтри.
Човечеството е толкова старо! Винаги трябва да вървиш по нечии стъпки.
Но хората са амбициозни и винаги се опитват да оставят своя отпечатък. Във всяка професия те са наследили такива, че е време да започнат да разчистват старите надеждни пътища.
Лариса Ратушная. Уралски геофизик, XX век.
1. Разностни оператори. Изолиране на шума в сигналите. Възстановете изгубени или липсващи данни. Апроксимация на производни.
2. Интегриране на данни. Алгоритми за интегриране по формули на трапец, правоъгълник, Симпсън.
Основният инструмент за проектиране на цифрови филтри е честотният (спектрален) анализ. Честотният анализ се основава на използването на периодични функции на синусите и косинусите. По същество спектралната характеристика на цифровия филтър е фина вътрешна структура на системата, нейният недвусмислен функционален паспорт на посоката на промяна на честотното съдържание на данните, което напълно определя същността на трансформацията на входните данни от филтъра.
Разгледайте примери за синтез и честотен анализ на филтри във връзка с известните методи за диференциране и интегриране на цифрови данни.
4.1. Разностни оператори /24/.
Примери за честотния подход при анализа на разностните оператори.
Операторът за разлика от първи редима формата:
Последователното n-кратно приложение на оператор се записва като оператор от n-ти ред:
Изходните стойности на импулсния отговор на диференциалните оператори към един импулсен сигнал на Kronecker са дадени в таблицата. Серии от последователни разлики съдържат биномни коефициенти с променлив знак. В представената форма операторите на разликата са причинно-следствени преместващи фази(едностранни) филтри, но е лесно да се види, че операторите с четна степен могат да бъдат преведени в симетрична форма чрез изместване наляво с половината прозорец на оператора.
Последният ред на таблицата показва усилването на дисперсията на шума, чиято стойност нараства рязко с увеличаване на реда на оператора. Това позволява използването на оператори за разлика с ред, по-голям от 1, за локализиране на статистически разпределени шумове в набори от данни. Тази възможност може да се види особено ясно в честотните характеристики на операторите.
Замествайки сигнала s(k) = exp(jk) в (4.1.1) и опростявайки, получаваме:
n s(k) = (j n )exp(jn/2) [2sin(/2)] n exp(jk).
H() = (j n ) exp(jn/2) [2 sin( /2)] n (4.1.2)
Тъй като модулът на първите два фактора в израз (4.1.2) е равен на 1, честотната зависимост на коефициента на пренос на диференциалния оператор се определя от втория фактор (2 sin(/2)) n и е показана на фигура 4.1.1.
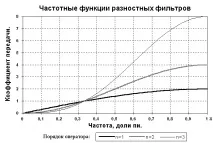
Ориз. 4.1.1. филтри за разлика.
Идентифициране на шума в сигналите.Както следва от графиките на фиг. 4.1.1, диференциалните оператори потискат DC компонента на сигнала и неговите хармоници в първата трета от интервала на Найкуист и увеличават високочестотните компоненти на сигнала в останалата част от интервала, колкото по-голям е редът на оператора. По правило тази част от основния интервал на спектъра на сигнала е заета от високочестотен статистически шум.
Шумът при анализа на данни може също да представлява определена информация, например за стабилността на условията на измерване и за влиянието на външни дестабилизиращи фактори върху измерванията. На фиг. Фигура 4.1.2 показва пример за подчертаване на интензивни шумови интервали в данните от акустичния регистър, което може да означава силенраздробяване на скали на тези интервали. Такава информация вече не се отнася до шума, а до много полезна информация при търсенето и проучването на нефт, газ и вода.
Възстановяване на изгубени данни.Разностните оператори имат една особеност: оператор от ред n+1 анулира полином от степен n, т.е. конволюцията на оператор от порядък n+1 с полином от степен n дава нулеви стойности: n+1 ③ Pn(k) = 0.
Тази функция може да се използва за създаване на много прости и сравнително надеждни оператори за възстановяване в масиви от липсващи и изгубени стойности или за замяна на стойности, отменени по време на обработката (например явни извънредни стойности).
Ако приемем, че сегментът от данни, съдържащ празнината, е полином от някаква степен, тогава конволюцията на данните с оператора на разликата от следващия ред трябва да бъде равна на нула. Така че, когато апроксимирате данни с полином от трета степен, за всяка точка в масива трябва да бъде изпълнено равенството:
Интерполационен филтър за възстановяване на загубена централна точка от данни:
Съответно операторът на филтъра за възстановяване на данни h(n) = (-1,4,0,4,-1)/6. Коефициент на усилване на шума 2 = 17/18 = 0,944.
Пример.Действителният сегмент от масива от данни: xk = .
Да приемем, че на сегмента е регистрирано явно отклонение: xk = .
Броят на изтласквания е отменен. Преброяване на заместване: x3 = (-x1+4x2+4x4-x5)/6= (-6+32+28-5)/6 8.17.
Петият брой е изгубен в масива. Възстановяване: x4 = (-x2+4x3+4x5-x6)/6 = (-8+32+20-3)/6 6,83.
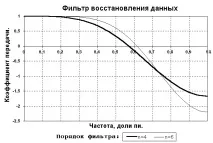
Ориз. 4.1.3. филтри за разлика.
Вземайки k = 0 в (4.1.3) и замествайки сигнала sk = exp(jk), получаваме честотната характеристика на филтъра за възстановяване на данни от 4-ти ред:
H() = (4 cos- cos 2)/3.
Тип честотна характеристика зафилтри за възстановяване на липсващи данни от 4-ти и 6-ти ред са показани на фиг. 4.1.3. Графиките ясно показват, че използването на филтри за интерполация на разликата за възстановяване на данни е възможно само за сигнали, чиито високочестотни компоненти са поне три пъти по-ниски от честотата на Найкуист. Интерполационни филтри по-високи от 4-ти ред не се препоръчват, т.к те имат усилване на шума по-голямо от 1.
На фиг. 4.1.4 - 4.1.6 са дадени примери за възстановяване на загубени данни във входните сигнали от оператора от 3-ти ред и спектрите на сигнала в сравнение с трансферната функция на оператора за възстановяване на данни.
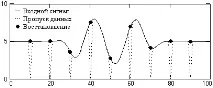
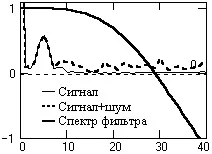
Ориз. 4.1.4. Възстановяване на нешумни данни. Фиг.4.1.5. Спектри.
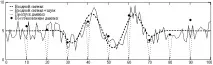
Ориз. 4.1.6. Възстановяване на шумни данни.
В сигналите, показани на фигурите, всеки 10-ти образец се губи (например по време на предаване на данни), като същевременно се запазва тактовата честота на номерирането на данните. Като се има предвид, че всички стойности на входните сигнали са положителни, нулевите стойности служат като индикатор за липсващи данни за работата на оператора. Във всеки друг случай трябва да се предостави специален маркер за оператора за възстановяване на данни (например за замяна на невалидни данни или извънредни стойности с определена висока или ниска стойност на проби).
Както следва от фиг. 4.1.5, спектърът на полезния сигнал е изцяло в зоната на коефициента на единица на честотната характеристика на оператора и възстановяването на данните се извършва почти без грешка (фиг. 4.1.4). Когато към сигнала се приложи статистически разпределен шум (фиг. 4.1.6), грешката при възстановяване на данни се увеличава, но за информационната част на пълния сигнал тя, както във входните данни, не надвишава средноквадратичната стойност (стандарт) на шумовите колебания.
Апроксимация на производни-Втората голяма област на приложение на диференциалните оператори. Оценките на първата, втората и третата производна могат да бъдат направени с помощта на най-простите формули за диференциране:
Първият производен оператор е нечетна функция и има въображаем спектър. Ако приемем s(t) = exp(jt), тогава истинската стойност на първата производна трябва да бъде: s'(t) = j exp(jt). Предавателна функция H() = j. Оценка на първата производна в точка n = 0 по отношение на диференциалния оператор при t = 1: s'(0) = (exp(j)-exp(-j))/2 = j sin = H1(). Съотношението на изчислената стойност към истинската стойност в същата точка: K1() = sin()/. Графиките на функциите в дясната половина на основния диапазон са показани на фиг. 4.1.7.
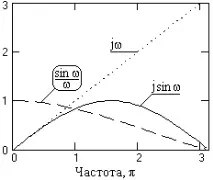
Както следва от горните изрази и графики, стойността на K() е равна на 1 само при честотата = 0. При всички останали честоти в интервала на Найкуист формулата дава подценени стойности на производните. Въпреки това, когато се обработват практически данни, последният фактор може да играе положителна роля, ако сигналът е нискочестотен (не повече от 1/3 от основния диапазон) и се регистрира на ниво високочестотен шум. Всяко диференциране повишава дела на неговите високочестотни компоненти в спектъра на сигнала. Печалбата на дисперсията на шума чрез диференциалния оператор на диференциация директно от неговия спектър в основния диапазон:
Kq= (1/)

С точна диференциация в целия основен диапазон:
Kq= (1/)

Следователно операторът на разликата има почти шест пъти по-малко усилване на дисперсията на шума от оператора на точното диференциране.
На фиг. 4.1.8 показва пример за разграничаване на хармоник с честота 0,1 честота на Найкуист (показана с пунктирана линия) и същия хармоникс насложен шум (плътна крива).
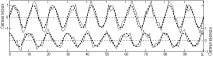
Ориз. 4.1.8. Пример за диференциране (входни сигнали отгоре, изходни сигнали отдолу).
Операторът за втора производна принадлежи към типа на четните функции. Честотна функция на оператора: H2() = -2(1-cos ). Собствена стойност на операцията H() = - 2 . Съотношението на действителната стойност към собствената
и също е равно на 1 само при честотата = 0. При всички други честоти в интервала на Найкуист формулата дава подценени стойности на производните, въпреки че те са по-малки в относителни стойности от оператора на първата производна. Честотните графики на диференциация са показани на фиг. 4.1.9. Усилването на дисперсията на шума от втория производен оператор е равно на 6 със собствена стойност на диференциация, равна на 19,5. Тези стойности показват, че операцията за двойно диференциране може да се приложи само към достатъчно добре обезшумени данни с основна енергия на сигнала в първата трета от интервала на Найкуист.
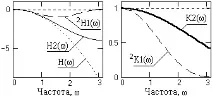
Ориз. 4.1.9. Честотни функции на оператор 2-ра производна.
По принцип втората производна може да се получи и чрез последователно двойно диференциране на данните от оператора на първата производна. За такива прости оператори обаче тези две операции не са идентични. Операторът на последователно двойно диференциране може да бъде получен чрез свиване на оператора на първата производна със себе си:
и има усилване на дисперсията на шума от само 0,375. Операторска честотна характеристика:
Графики 2 H1() и коефициент на съответствие 2 K1() са показани с пунктирани линии на фиг. 4.1.9. От сравнението им с графиките на втората производна се вижда, че последователното двойно диференциране е възможно само за данни, чийто спектрален състав заема не повече от една пета от началната част на главниядиапазон и е по-лош от оператора за втора производна по отношение на точността.
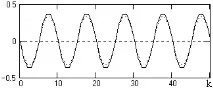
Ориз. 4.1.10. Втората производна на хармоника с честота при t=1
(пунктирана линия - двойно последователно диференциране)
Пример за прилагане на два оператора на втората производна е показан на фиг. 4.1.10.
Честотата на Найкуист на основния диапазон е обратно пропорционална на интервала на дискретизация на данните t (N = /t) и следователно интервалът на дискретизация на данните за правилното използване на прости оператори за диференциране трябва да бъде 3-5 пъти по-малък от оптималния за сигнали с известни гранични честоти на спектралния състав.
Предлага се честотните функции за третата производна да бъдат получени независимо.