дескриптивна геометрия
Построяване на профилна проекция на конична повърхнина. Изградете проекции на линиите на пресичане на проходния разрез върху повърхността на конуса. Определете видими и невидими линии. Конструирайте разработка на страничната повърхност на конус с нарез.
Построяване на профилна проекция на конична повърхнина. Определете видими и невидими точки.
На диаграмата коничната повърхнина се определя от границата (очертаваща образуваща) и линията на пресичане на коничната повърхнина със съответната главна проекционна равнина (следа от коничната повърхнина). Така коничната повърхност е изобразена като два триъгълника и кръг, както е показано на фигурата.
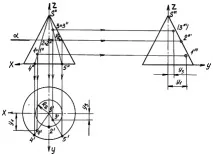
Точка върху повърхността на конус може да бъде конструирана по два начина: като се използва образуваща на конуса, минаваща през точката, и като се използва паралел Паралелът е права, която лежи върху следата на сечаща равнина α, успоредна на основата на конуса. Паралелът върху хоризонталната равнина на проекциите е изобразен като окръжност, чийто радиус е равен на разстоянието от оста на симетрия на конуса до крайната точка на граничната генератриса на конуса. Фронталните проекции на точки 1, 2, 3 съвпадат със самите точки, които лежат на повърхността на конуса. Хоризонталните проекции на точки 1', 3' се намират с помощта на генератори, начертани през точки 1 и 3 . Челният генератор през точка 1 се конструира с помощта на точки S" и 4" , а през точка 3 - с помощта на точки S" и 5" . Изграждаме хоризонтални проекции на точки 4' и 5' по линиите на комуникация, които лежат върху големия кръг на основата на конуса и ги свързваме с точката S'. Получаваме хоризонталните проекции на образуващите S' 4', S'5' . От точки 1" и 3" спускаме комуникационните линии надолу до пресечната точка с хоризонталните проекции на генераторите S' 4' и S' 5' и получаваме хоризонталните проекции на точките 1' и 3' . Хоризонталната проекция на точка 2' се изгражда с помощта на паралел. За целта през точката 2'', успоредна на основата на конуса, се прекарва секуща равнина a и върху хоризонталната проекция се построява проекция на успоредника - окръжност с радиус R2. Хоризонталната проекция на точка 2' ще бъде в пресечната точка на тази окръжност с линията на свързване от точка 3". Профилните проекции на точките 1'', 2'''', 3'''' се определят с помощта на разстоянието във всяка точка от оста на симетрия на конуса X, измерено върху хоризонталната проекция на конуса. Тези разстояния y се нанасят върху профилната проекция на конуса от оста на симетрия Z върху съответните свързващи линии на точките.
На диаграмата на конуса се разграничават видимите и невидимите части на повърхността. Точките, разположени върху хоризонталната проекция на конуса под оста X (1',2',3') и точките, разположени върху профилната проекция на конуса вдясно от оста на симетрия Z (1'',2'',3''), ще бъдат видими на фронталната проекция. Точките, разположени върху хоризонталната проекция на конуса над оста X, и точките, разположени върху профилната проекция на конуса вляво от оста на симетрия Z, ще бъдат невидими на фронталната проекция. Виждат се точките на хоризонталната проекция на конуса. Точките, разположени на хоризонталната проекция на конуса вляво от оста на симетрия Y (1',2'), и точките, разположени на фронталната проекция на конуса вляво от оста на симетрия Z (1,2"), ще бъдат видими на профилната проекция на конуса. Точките, разположени на хоризонталната проекция на конуса вдясно от оста Y на симетрия (3') и точките, разположени на фронталната проекция на конуса вдясно от оста на симетрия Z (3"), ще бъдат невидими в проекцията на профила (3'') .
Изградете проекции на линиите на пресичане на проходния разрез върху повърхността на конуса. Дефинирайте видими и невидими линии.
а) представете си, че α1, α2, α3, α4 -спомагателни режещи равнини, образуващи проходен разрез в конуса (фиг. B.6). Нека обозначим входните и изходните точки на изреза върху повърхността на конуса, съответно, 11-12, 21-22, 31-32, 41-42, 51-52, 61-62, 71-72, 81-82. Тези точки се образуват в резултат на пресичането на образуващите на конуса със следите на равнините α1, α2, α3, α4; b) дефинирайте проекциите на маркираните точки. Предните проекции на точките съвпадат със самите точки. Хоризонталните проекции на точки лежат в пресечната точка на хоризонталните проекции на генераторите, начертани през точки с комуникационни линии. Хоризонталните проекции на точки 11, 12 и 5'1, 5'2 се определят с помощта на паралели. За да направите това, през точката и 1''1 - 1''2 се начертава режеща равнина α5, успоредна на основата на конуса, и радиусът на паралела R1 се измерва от оста на симетрия на конуса до крайната точка на граничната образуваща на конуса. Върху хоризонталната проекция на конуса с радиус R1 е начертана окръжност, която при пресичане с комуникационната линия от точки 1''1 и 1''2 ще изгражда хоризонтални проекции на точки 1''1 и 1''2. Точки 5''1= 5''2 и 4''1 = 4''2 лежат в равнината α3, която определя радиуса на паралела R5. Върху хоризонталната проекция на конуса с радиус R5 е начертана окръжност, която при пресичане със съобщителни линии от точки 5''1 , 5''2 и 4''1 , 4''2 ще изгради хоризонтални проекции на точки 5'1 и 5'2, 4'1 и 4'2 . Профилните проекции на точки се изграждат с помощта на координатите на всяка точка, които се нанасят от коничната ос на симетрия Z върху профилната проекция върху съответните комуникационни линии на всички точки. На фиг. B.6 показва конструкцията на профилни проекции на точки 4'"1 и 4'"2. Получените проекции на точки трябва да бъдат свързани с гладка линия една с друга в последователността, както са посочени на челната проекция на конуса;
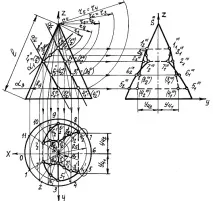
в) определят видимостта на точките. Включенохоризонтална проекция на конуса, всички точки са видими. Но вътре в конуса има невидими линии на пресичане на секущите равнини. Това са пресечните линии на равнините α1 и α2 (11-12), равнините α1 и α4 (71-72), равнините α3 и α4 (51-52), равнините α3 и α2 (41-42). Следователно върху хоризонталната проекция на конуса е необходимо точките 1'1, 1'2, 4'1 и 4'2, 7'1 и 7'2, 5'1 и 5'2 да се свържат с пунктирана линия. Част от линията 5'1 и 5'2 от точка 1'1 до точка 5'1 и от точка 1'2 до точка 5'2 ще бъде видима. На проекцията на профила всички тези линии ще бъдат невидими. Трябва да се отбележи, че частта от граничната образуваща на конуса между точките 1'''1 и 5'''1 , 1'''2 и 5''''2 ще изчезне. На профилната проекция на конуса има невидими точки, това са точки 21 и 22, 31 и 32, 41 и 42, които са разположени на хоризонталната проекция вдясно от оста на симетрия Y. Но тъй като координатите на точки 7''''1 и 7'''2 се оказаха по-малки от координатите на точки 2''''1 и 2''''2, тогава точки 2''''1 и 2''''2 се оказаха видими и участъкът от кривата линия от точки 1''''1 и 1''''2 до кривата линия, образувана от точки 51.2, 61.2, 71.2, става видима.
Конструирайте развитие на страничната повърхност на конуса
Построяваме сектор с радиус r = l, където l е дължината на образуващата на конуса. Съставяме дъгата на сектора от 12 секции и ги обозначаваме с числата 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0. Разстоянието между числата е равно на хордата, измерена между същите числа по обиколката на основата на конуса, която е разделена на 12 равни части. Точките, отбелязани с цифрата 0, се свързват с линия с точката S - върха на конуса и се получава разработка на страничната повърхност на конуса, към която трябва да се пренесат входната и изходната точки на проходния разрез. Например, нека изградим точки 51 и 52, които се намират на образуващата на конуса, обозначена с числата 3 и 9.
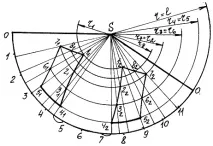
При развитието свържете точки 3 и9 с горни S линии. Then we transfer points 51 and 52 along the line of communication on the frontal projection to the boundary generatrix of the cone and from point S "measure the radius r5, which determines the natural value of the distance from point S to points 51 and 52 on the development of the cone. With this radius r5 we draw an arc from point S to the intersection with generatrix 3 and 9. Points 41 and 42 will also be located on this radius. Let's determine the position of the generators for these points. On the horizontal projection of the cone through the point S ' and points 41 ' and 42 ' let's draw the projections of the generators of these points to the intersection with the circumference of the base of the cone. Then we measure the distance along the chord from the points of intersection of the generatrix with the circle to the nearest figure on this circle and plot these distances from the digitized sector on the sweep. Point 41 ' lies in the sector between the numbers 4 and 5, and point 42 ' lies in the sector between the numbers 7 and 8. We connect the obtained points on the arc with radius r with the vertex S by a line and at the intersection of these lines with a circle with radius r4 we get points 41 and 42. The principle of constructing other points of the through cut on the development is similar. След като са изградили точки върху развитието на конуса, те трябва да бъдат свързани с гладка извита линия.