Двойни графики
Дефиниция 19 (Двойна графа).Граф, чиито върхове са лицата на графикатаG, изобразени на повърхността, ръбовете са ръбовете на графикатаG, лицата са върховете на графикатаG, връзката на инцидентност е връзката на ограниченост на графикатаGи връзката на ограниченост е отношението на инцидентност на графикатаG, се наричадвойна графакъм графика G.
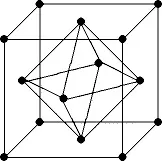
За политопите отново има много визуален начин за получаване на двойни графики. Състои се от следното. В центъра на всяко лице се поставя точка - такива точки ще бъдат върховете на двойната графика. Ръбовете трябва да свързват онези върхове, чиито лица са разделени от ръбове в оригиналната графика. Резултатът е полиедър, вписан в оригиналния. Освен това, ако оригиналната графика е правилен (полуправилен) полиедър, то двойственият също ще бъде правилен (полуправилен).
Пример 7 (двойна графика).Фигурата показва двойните графики на куб и октаедър.
Пътища на Ойлер, Хамилтонови пътища.
Пътят на Ойлерв графика е произволен път, минаващ през всеки ръб на графиката точно веднъж, т.е. пътv1, .vm+1така че всяко реброeEсе появява в последователносттаv1, . vm+1точно веднъж катоe=i, vi+1>за някоиi.
Акоv1= vm+1, тогава този път се наричаОйлеров цикъл. Проблемът за съществуването на Ойлеров път в даден граф е решен от Ойлер през 1736 г. и представеното от него необходимо и достатъчно условие за съществуването на такъв път се счита за първата теорема в теорията на графите в историята.
Теорема.Тогава съществува Ойлеров път в графикатаи то само ако графът е свързан и съдържа най-много два върха с нечетна степен.
Доказателство. Доказателството за достатъчността на условието на теоремата ще бъде следствие от анализа на алгоритъма за намиране на пътя на Ойлер, който ще бъде описан по-долу. Необходимостта от условието е очевидна, тъй като ако връхv, който е различен от върхаv1иvm+1, се появи в пътя на Ойлерkпъти, то това означава, че степента на този връх в графиката е 2k. От това следва, че върхове с нечетна степен, ако съществуват, са краищата на пътя на Ойлер. Тук трябва да се отбележи, че няма графи само с един връх с нечетна степен. Наистина, обозначавайки степента на връхvсd(v), имаме
защото в посочената сума всяко ребро u,v>се брои два пъти: веднъж вd(u) и веднъж вd(v). От това следва, че броят на върховете винаги е четен.
Ако в свързана графа няма върхове с нечетна степен, тогава всеки път на Ойлер е цикъл, тъй като краищата на път на Ойлер, който не е цикъл, винаги са върхове с нечетна степен.
Да приемем, чеuиvса единствените върхове с нечетна степен в свързан графG=V,E, и образувайте графG*чрез добавяне на допълнителен връхtи ръбове u,t>и v,t >(или само u,v>ако u,v>E). ТогаваG*е свързан граф без върхове с нечетна степен и пътищата на Ойлер вGще бъдат в очевидно едно-към-едно съответствие с циклите на Ойлер вG*. Поради това по-нататък ще се занимаваме само с цикли на Ойлер.
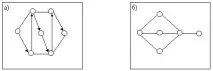
Пример за Хамилтонов път в графика и график, в който такъв път не съществува, е показан на фиг. (a), (b) съответно.
За разлика от пътищата на Ойлер, няма нито едно просто необходимо и достатъчно условие за съществуването на пътища на Хамилтон, въпреки факта, че този проблем е един от най-централните в теорията на графите.
Проблемът за съществуването на Хамилтонов път принадлежи към класа на така нареченитеNP-пълни проблеми.Това е широк кръг от проблеми, включително фундаментални проблеми от теорията на графите, логиката, теорията на числата, дискретната оптимизация и други дисциплини, нито една от които не е известна с полиномен алгоритъм (т.е. с броя на стъпките, ограничени от полином в размерността на проблема).
Намиране на най-кратките пътища в графика
Ще разгледаме насочени графиG=V,E, чиито дъги са претеглени. Това означава, че всяка дъгаu,vEе свързана с някакво реално числоa(u,v), нареченотеглона тази дъга.
Ако последователността от върховеv0,v1.vpдефинира път вG, неговатадължинасе определя като сумата
(Обърнете внимание, че ако в произволна графика вземем теглото на всяка дъга равно на единица, тогава получаваме обичайната дефиниция на дължината на пътя като броя на дъгите; дължината на пътя е 0, когатоp= 0).
Ще се интересуваме от намирането на най-краткия път между фиксирани върховеs,tV. Ще обозначим дължината на такъв най-кратък пътd(s,t) и ще наречемразстояниетоотsдоt(разстоянието, определено по този начин, може да бъде отрицателно). Ако няма път отsдоt, тогава поставямеd(s,t) =╔. Ако всеки контур на нашата графика има положителна дължина, тогаванай-късиятпът винаги ще бъдеелементаренпът, т.е. Vпоследователностиv1.vpняма да се повтаря.
От друга страна, ако графът има контур с отрицателна дължина, тогава разстоянието между някои двойки върхове става неопределено, тъй като обикаляйки този контур достатъчен брой пъти, можем да покажем пътя между тези върхове с дължина, по-малка от произволно реално число. В този случай може да се говори за дължината на най-краткия елементарен път, но проблемът, поставен по този начин, вероятно ще бъде много по-сложен, тъй като по-специално съдържа проблема за съществуването на хамилтонов път.
Могат да бъдат дадени много практически интерпретации на проблема за най-краткия път.Например, върховете могат да съответстват на градове и всяка дъга може да съответства на някакъв път,дължинатана който е представена от теглото на дъгата. След това търсим най-кратките пътища между градовете. Теглото на една дъга може също да съответствана цената(иливремето) за прехвърляне на информация между върховете. В този случай ние търсим най-евтиния (или най-бързия) начин за прехвърляне на информация. Друга ситуация се получава, когато теглото на дъгата u,vе равно навероятността p(u,v) за безпроблемна работа на канала за предаване на информация. Ако приемем, че отказите на канала не зависят един от друг, тогава вероятността за изправност на пътя за предаване на информация е равна на произведението на вероятностите на съставните му дъги. Проблемът с намирането на най-надеждния път може лесно да бъде сведен до проблема с най-краткия път чрез замяна на теглатаp(u,v) сa(u,v) = - logp(u,v).
Първо, разгледайтеалгоритми за намиране на разстоянието между върховете, а не самите пътища. Въпреки това, знаейки разстоянието, можем лесно да определим най-кратките пътища, при условие че дължината на всички контури е положителна. За товадостатъчно е да се отбележи, че за произволниs,tV(s╧t) съществува връхvтакъв, че
Наистина, предпоследният връх на произволен най-кратък път отsдоtима това свойство.
Тъй като дължината на всички контури е положителна, лесно следва, че последователносттаt,v,u, . не съдържа повторения и завършва с връхs.
Очевидно той определя (когато редът е обърнат) най-краткия път отsдоt.
Най-кратките пътища от фиксиран връх
Повечето от известните алгоритми за намиране на разстоянието между два фиксирани върхаsиtсе основават на действия, които могат да бъдат широко представени по следния начин: за дадена матрица за тегло на дъгатаA[u,v],u,vV, някои горни ограниченияD[v] към разстояния отsдо всички върховеvV. Всеки път, когато задаваме това
D[u] +A[u,v] 2 ) - случаят, когато графиката е без контур (теглата на дъгата могат да бъдат произволни). Първо доказваме следната лема.
Лема.В произволен безконтурен граф върховете могат да бъдат преномерирани по такъв начин,че всяка дъга ще има форматаvi,vj,къдетоi4 ) (използвайки метода на Форд-Белман) или O(n3 ) за безконтурни графики или неотрицателни тегла. Оказва се обаче, че в общия случайn-кратното използване на метода на Ford-Bellman не е най-добрият метод. Нека да разгледаме два по-ефективни метода.
(1)
dij (m+1) = minik (m) + akj: 1 (m+1) ] е "произведението" на матриците [dij (m) ] иA= [aij]. Обозначететакъв „продукт“ от две матрициAиBот гледна точка наA*Bи имайте предвид, че за тази операция елементът за идентичност е матрицата
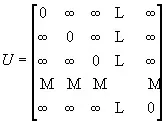
Уравнения (1) и (2) сега лесно предполагат, че [dij (0) = U] и
Възможен е един от следните случаи:
(2) dij (n-1) ╧dij (n) . Това означава, че има път с отрицателна дължина.
ПродуктътA*Bот двеn╢nматрици може да бъде изчислен за O(n3 ) време (nдобавяния иn- 1 сравнения за всеки отn2 елемента отA*B). Следователно, матрицата [dij (n-1)] и по този начин разстоянието между всички двойки върхове могат да бъдат изчислени за O(n4) време.
нека въведем терминологията и в същото време сравним насочени и ненасочени графики епистемологично, представяйки паралелни места двуезично - под формата на следната таблица. Диграфът тук и по-долу е насочен график.
ГРАФИКИ И ОРИЕНТИРАНИ ГРАФИКИ (АНАЛОГИИ И РАЗЛИКИ)