екстремен експеримент
Задачата на планирането на екстремен експеримент е да се сведе до минимум броят на експериментите, като същевременно се намерят оптимални условия. Например, необходимо е да се намери температурата на ненагряване на заготовките и скоростта на деформация, които осигуряват минималната цена на изковките при горещо изотермично коване
Най-простият метод за планиране на експеримент е провеждането на тестове с всички възможни комбинации от фактори (метод на груба сила). Но дори и при двуфакторен експеримент, за да се получи пълна картина, е необходимо да се проведат голям брой тестове. Ето защо при решаването на експериментални задачи често се използва следният метод: чрез промяна само на един фактор (останалите остават постоянни) се намира определен екстремум за този фактор; след това последователно определете следващите крайности чрез промяна на втория, третия и следващите фактори. Процедурата се повтаря до достигане на оптимума за всички фактори (Фигура 27).
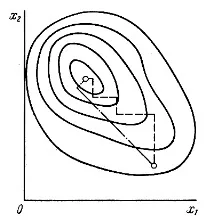
Фигура 27. Търсене на оптималната зона чрез последователно определяне на частични оптимуми (пунктирани линии) и метода на стръмно изкачване (пунктирани линии); твърд
са показани редове с еднакво ниво на оптимизираната функция
Такава схема води до значително намаляване на броя на експериментите, но също така не е оптимална и понякога води до намиране на фалшиви екстремуми.
Характеристиката на целта в екстремен експеримент, дадена количествено, се нарича оптимизационен параметър. Параметърът за оптимизация е отговор на влиянието на фактори - независими променливи. Резултатите се използват за получаване на математически модел - система от математически зависимости, които описват изследвания процес. В конкретен случай това е уравнение, свързващо параметъра за оптимизация с факторите. Такивауравнението се нарича още функция на отговора.
Най-общо функцията на отговор може да бъде представена чрез израза
къдетоxiса независими променливи (фактори).
Функцията на отговор, ако е неизвестна от теорията, може да бъде представена например чрез полином от формата
където biе регресионният коефициент.
Въз основа на резултатите от експеримента е възможно да се определят само примерни регресионни коефициентиbi, които са само оценки на теоретичните коефициенти bi. На първия етап, за да се определи посоката на движение към оптимума и стръмно изкачване по повърхността на реакцията, функциите на реакция се изразяват с полином от първа степен
За да се определят коефициентите на това уравнение, е необходимо да се приложи факторен експеримент от тип 2k. Плановете за такъв експеримент се наричат планове от първи ред. Стръмното изкачване завършва след достигане на оптималната област, която най-често се описва с полином от втора степен:
За да се определят всички коефициенти на това уравнение, е необходимо да се приложи план на експеримент, в който всеки фактор варира най-малко на три нива. Такива планове се наричат планове от втори ред.
И така, стратегията на метода при изследване на повърхността на реакцията с цел намиране на екстремума е следната. Въз основа на малка поредица от експерименти се намира локално описание на повърхността на реакция в някаква първоначална област, като се използва линеен модел. В центъра на областта се изчислява линейна апроксимация на градиента, а в посоката на градиента, т.е. в посоката на най-стръмното изкачване (стръмно изкачване), се провеждат експерименти, докато се достигне стационарен регион, в който се намира екстремумът. Ако намереното линейно приближение на градиента за центъра на региона се различава значително от стойността на градиента в дадена точка попосока на движение, може да се намери ново описание на повърхността на реакция, като се използват полиноми от първи ред в близост до тази точка и може да се изчисли нова стойност на градиента. В стационарната област линейният модел вече не е адекватен и като правило се използват полиноми от втора и дори трета степен за описание на повърхността на реакция в тази област. В стационарния регион са необходими повече експерименти, тъй като тук е необходимо да се получи възможно най-точното описание.
къдетоi, jса единични вектори по протежение на променливите осиx.
Този вектор е перпендикулярен на повърхността с равно нивоy=const и показва посоката на най-стръмното изкачване (стръмно изкачване). Ако моделът е линеен, тогава коефициентитеbiса координатите на градиентния вектор. Ако факторите се променят пропорционално на получените оценки на тези коефициенти, тогава се осъществява движение в посока на най-бързото приближаване към оптимума.
Компонентите на градиента на експериментално получения линеен модел зависят от основното ниво и интервалите на изменение на променливите.
Пълен факторен експеримент
Решаването на проблема за оптимизация започва с избора на областта на експеримента въз основа на априорна информация. В областта на експеримента се установяват основните нива и интервали на изменение на факторите. Основното или нулевото ниво на фактора е неговата стойност, взета за първоначална по отношение на експеримента. Дизайнът на експеримента се състои в избора на точки, които са симетрични по отношение на началната точка.
Интервалът на вариация на фактора е число, добавянето на което към основното ниво дава горното ниво на фактора (съответно долното ниво). Факторните нива кодират:
Хi=
където е естествената стойност на фактора; интервал на вариация (по-често -половин интервал).
Експеримент, в който се реализират всички комбинации от нива, се нарича пълен факторен експеримент. Ако броят на нивата еm, а броят на факторите е k, тогава общият брой експерименти (с изключение на дублирани или паралелни експерименти)
С линеен моделN=2k.
Факторният експеримент се провежда с помощта на планираща матрица. Например, за два фактора, матрицата за планиране е показана под формата на таблица. 1. Броят на редовете в матрицата е равен на броя на експериментите. Кодираните стойности на факторите са съкратени: + или -.
Матрица за планиране с 2 фактора
| номер опит | x1 | x2 | при |
| - + - + | - - + + | y1 y2 y3 y4 |
За да се движите по градиент, първо се нуждаете от линеен модел. Сk=2
Стойностите на коефициентите в това уравнение се определят с помощта на стойностите на функцията за отговор. Те са три, а експериментите са 4. Разликата между броя на експериментите и броя на коефициентите на модела се нарича брой степени на свобода
Броят на степените на свобода може да се използва за проверка на адекватността на модела.
Стойността и знакът на коефициента в регресионното уравнение показват приноса на този фактор към общия резултат.
Линеен е ефектът, който характеризира линейната зависимост на оптимизационния параметър от съответния фактор. Ефектът от комбинираното въздействие на няколко фактора се нарича ефект на взаимодействие. Като се вземе предвид ефектът на взаимодействие с броя на факторитеk=2(Таблица 2):
Тукx0 е колона с фиктивна променлива. Въвежда се за оценка на стойносттаb0.
Матрица на планиране, отчитаща ефекта от взаимодействието
| номер опит | x0 | x1 | x2 | x1x2 | при |
| + + + + | - + - + | - - + + | + - - + | y1 y2 y3 y4 |
За да изградите план от матрици с голям брой фактори, можете да използвате следната техника. В първата колона x знаците се сменят последователно, във втората - след 2, в третата - след 4 и т.н.
Експеримент с дробен фактор
За да се намали броят на експериментите в линеен модел от тип 2 2, може да се вземеb12=0 и матричната колонаx1x2 може да се използва за третия факторx3. Тогава
За да се определят коефициентите на това уравнение, е достатъчно да се извършат 4 експеримента вместо 8 в пълен факторен експеримент от тип 2 3 . План за експеримент, който предвижда изпълнението на половината от експериментите, се нарича полуреплика. Дробните реплики означават 2k-p, къдетоpе броят на линейните ефекти, приравнени на ефектите на взаимодействие. Прир=2 се получава ¼-реплика,р=3 –1/8-реплика. Репликите, използвани за намаляване на експериментите с 2mпъти, се наричат регулярни.
Поради факта, че в частични реплики част от взаимодействията се заменят с нови фактори, намерените коефициенти на регресионното уравнение ще бъдат съвместни оценки на линейни ефекти и ефекти на взаимодействие. Такива оценки се наричат смесени. Препоръчва се линейните ефекти да се бъркат с онези взаимодействия, които според априорната информация са незначителни.
Броят на несмесените ефекти в частична реплика се нарича нейна резолюция.
Често се налага да се решават задачи, при които предварително може да се приеме, че ефектите на взаимодействие, макар и малки в сравнение с линейните, все пак не са равни на нула. В такива случаи е необходимо предварително да се определи кои коефициенти са смесени оценки. След това, в зависимост от условията на задачата,се избира такава дробна реплика, с помощта на която е възможно да се извлече максимална информация от експеримента.
Директната оценка на разделителната способност на частична реплика е трудна. Следователно частичните реплики се определят с помощта на генериращи релации. Съотношение, което показва кое от взаимодействията се приема за незначително и се заменя с нов фактор (x3=x1x2, например), се нарича генериращо.
Частична реплика, получена чрез замяна на всички ефекти на взаимодействие с нови фактори, се нарича наситена. Адекватността на модела в този случай не може да бъде проверена, тъй като броят на степените на свобода е нула.
Свойства на пълни и дробни факторни матрици
1. Симетрия спрямо центъра на експеримента - алгебричната сума на елементите на колоната на всеки фактор е равна на нула:
,
къдетоϳ– номер на опит;i– номер на фактора.
2. Свойство за нормализиране: сумата от квадратите на елементите на всяка колона е равна на броя на експериментите:
.
3. Свойството ортогоналност - сумата от произведенията ред по ред на елементите на всеки две колони е равна на нула:
,
Ортогоналността на матрицата дава възможност да се оценят всички коефициенти на регресионното уравнение независимо един от друг. Ако някой коефициент на регресия се окаже незначителен, той може да бъде отхвърлен, без да се преизчислява останалата част.
4. Свойство на въртене: точките в матрицата за планиране са избрани така, че математическият модел, получен от резултатите от експеримента, да е в състояние да предскаже стойностите на оптимизационните параметри със същата точност във всяка посока на равни разстояния от центъра на експеримента.