ФОРМУЛА НА ГРИЙН
ФОРМУЛА НА ГРИЙН - формули за интегралното смятане на функциите на много променливи, свързващи стойностите на n-кратния интеграл върху областта D на n-мерното евклидово пространство E n и (n-1)-кратния интеграл върху частично гладката граница ∂D = T на тази област. G. f. се получават чрез интегриране по части на интегралите на дивергенцията на векторно поле, което е непрекъснато в D̅ = D + Г и непрекъснато диференцируемо в D.
В най-простия G. f.
криволинейният интеграл по контура Г се изразява чрез двойния интеграл по областта D ⊂ E 2 . В този случай домейнът D е ориентиран по естествен начин и се приема индуцирана ориентация на границата на Γ, известна като байпас обратно на часовниковата стрелка. Формула (1) има проста хидродинамика смисъл: потокът през границата на област G на течност, протичаща по равнина със скоростv= (Q, -Р) е равен на интеграла по област D на интензитета (дивергенцията) divv= ∂Q/∂x - ∂P/∂y на източниците и поглътителите, разпределени в D. В този смисъл G. f. (1) е подобна на формулата на Остроградски (виж също формулата на Стокс).
Формула (1) понякога се нарича. от имената на К. Гаус (S. Gauss) и Б. Риман (V. Riemann). Нито едно от използваните имена не е исторически коректно: формула (1) е открита още в анализа от 18 век. - Л. Ойлер (L. Euler) и др.
J. Green [1] притежава следния H. f. потенциална теория
- подготвителен G. f. И
където D - площ E 3, x \u003d (x 1, x 2, x 3), dx \u003d dx 1 dx 2 dx 3 - обемен елемент G, ds - площен елемент G, N \u003d (N1, N2, N3) - единица външна (co) нормална към G,
е операторът на диференциране по посока на (ко)вектора N, и
Формули (2), (3) са валидни и в случая, когато D е площ E n , x = (x 1 , . x n ), dx = dx 1 . dx n - обемен елемент D, ds - елемент от (n-1)-мерен обем Г, и
- операторЛаплас с n независими променливи. Обобщения на G. f. (2) и (3) за линейни частични диференциални оператори с достатъчно гладки коефициенти имат формата:
- (реални) спрегнати диференциални оператори от втори ред, a ij = a ji, тогава
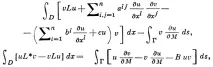
където N = (N1, .Nn) е единичният (ко)вектор на външната нормала към Γ,
- операторът на диференциране по посока на т.нар. connormals
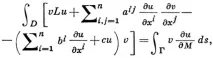
където M е коннормал на оператора L, a
- (реални) спрегнати диференциални оператори от ред m, α=(α1, α2, . αp) - целочислен мултииндекс с дължина α = p, 1 ≤ αi ≤ n, Dα = ∂α1∂α2 . ∂αp, ∂ = ∂/∂x i тогава
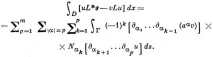
Тук граничният интеграл може да бъде записан като билинейна сума
където Si, Tj са някои линейни диференциални оператори от порядъци si, tj, 0 ≤ si + tj ≤ m - 1.
G. f. играят важна роля в анализа и особено в теорията на граничните задачи за диференциални оператори (обикновени и с частни производни) от втори и по-високи редове. За функции u(x), v(x), достатъчно гладки в D̅, G. f. (2), (4) служат като източник на редица отношения, полезни за изучаване на свойствата на решаване на гранични задачи, изясняване на вида на граничните задачи, получаване на решения в явна форма и т.н. Например, за хармонична функция u(x) в D, от (2) с v(x) = 1 следва теоремата на Гаус:
За функции u(х), w(x) достатъчно гладки в D̅ и функции
което за x = y има същата особеност като фундаменталното решение на оператора на Лаплас, следните G. функции са верни:
и ωn = 2π n/2 /Г(n/2) е площта на (n - 1)-мерната единична сфера на пространството E n . Освен това, за y ∈ Γ се приема, че границата на Γ има непрекъсната допирателна равнина в някаква околност на y.
Формули (5) и (6) служат като основа за получаване на интегралпредставяния на решения на основните гранични проблеми на теорията на потенциала (виж Хармонична функция, функция на Грийн, формула на Поасон). Например оттук за хармоничната функция u(x) в D получаваме формулата или интеграла на Грийн
който играе важна роля в теорията на хармоничните функции.
Формули, подобни на формули (5), (6), които дават интегрални представяния на решението на задачата на Коши или смесена задача, също са валидни за нормално хиперболични. оператор от втори ред. Вижте формула на Кирхоф, метод на Риман, функция на Риман.
Относно G. f. в теорията на граничните проблеми вижте също [4] -[9].
Лит.: [1] Грийн Г., Есе за приложението на математическия анализ към теориите за електричеството и магнетизма, Нотингам, [1828]; [2] Максуел Д., Избрани трудове по теория на електромагнитното поле, прев. от англ., М., 1954; [3] В. И. Смирнов, Курс на висшата математика, т. 2, 20 изд., М., 1966; [4] Р. Курант, Частични диференциални уравнения, прев. от англ., М., 1964; [5] В. С. Владимиров, Уравнения на математическата физика, 2-ро издание, Москва, 1971 г.; [6] С. Л. Соболев, Уравнения на математическата физика, 4 изд., Москва, 1966 г.; [7] Миранда К., Частични диференциални уравнения от елиптичен тип, прев. от италиански., М., 1957; [8] N. Dunford и J. T. Schwartz, Линейни оператори, прев. от английски, част 2, М., 1966; [9] J.-L. Lyonet и E. Magenes, Inhomogeneous Boundary Value Problems and Their Applications, прев. от френски, Москва, 1971г.
А. К. Гушчин, Л. П. Купцов.
- Математическа енциклопедия. T. 1 (A - D). Изд. колегия: И. М. Виноградов (главен редактор) [и др.] - М., "Съветска енциклопедия", 1977, 1152 stb. от болен.