Графично представяне на вариационната серия
Графичното представяне на резултатите от измерването се изразява в изграждането на три графики:честотен полигон (фиг. 1),хистограми (фиг. 2) икумулативен честотен полигон (сумарна крива иликумулативен ) (фиг. 4).
Честотен полигон ихистограма показват разпределението на измерените показатели и групирането им около средната стойност.
За да се изградимногоъгълник в декартови координати, средните стойности на интервалите се нанасят по абсцисната ос, а съответните честоти (или честоти) се нанасят по ординатната ос.
 |
Ориз. 1. Многоъгълник на честотните резултати
За да се изградихистограма, границите на интервалите се нанасят по абсцисната ос и върху тях се възстановяват правоъгълници до честотното ниво, съответстващо на интервалите, нанесени по ординатната ос (фиг. 2).
 |
Ориз. 2. Хистограма на разпределението на резултатите
Ако поставим многоъгълник на разпределение на честотата върху хистограмата с пунктирана линия, тогава ще получим първоначална представа за функцията на диференциалното разпределение.
По този начин,теоретичният аналог на хистограмата е плътността на разпределение на вероятностите или диференциалната функция на разпределение (фиг. 3).
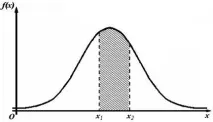
Ориз. 3. Плътност на вероятността
С други думи, хистограмата еекспериментален аналог на плътността на разпределението на вероятностите.
Площта на хистограмата е равна на сумата от всички честоти, т.е. размера на извадката, или сумата от честотите, т.е. единица.
Многоъгълник на натрупаните честоти показва нарастването на показателите от интервал на интервал, поради което се нарича ощесумарна крива иликумулативно. За да се построи полигон от натрупани честоти, по абсцисната ос се нанасят горните граници на интервалите, а по ординатната ос - съответните натрупани честоти (или натрупаните честоти) (фиг. 4).
 |
Ориз. 4. Многоъгълник на натрупаните честоти на резултатите
Теоретичният аналог на многоъгълника на натрупаните честоти на резултатите е функцията на разпределение или интегралната функция на разпределение (фиг. 5).
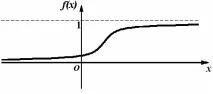
Ориз. 5. Разпределителна функция
С други думи, многоъгълникът на натрупаните честоти на резултатите еекспериментален аналог на функцията на разпределение.
По този начин графичното представяне на резултатите от измерването разкрива моделите на тяхното разпределение и ви позволява правилно да изберете последващите статистически характеристики за по-нататъшен анализ на получените експериментални данни.
Въпреки това, преди да продължим с по-нататъшни изчисления, си спомняме нормалния закон за разпределение.
Нормално разпределение
Повечето експериментални изследвания не само в областта на физическата култура и спорта, но и в биологията, медицината и т.н. са свързани с измервания, резултатите от които могат да приемат всякакви стойности в даден интервал и се описват чрез модел на непрекъснати случайни променливи, които са обект на определен закон на разпределение.
Сред всички непрекъснати закони на разпределение на вероятностите,нормалното разпределение, илиразпределението на Гаус, като най-често срещаният тип разпределение, заема специално място.
Нормалният закон за разпределение се изразява със следната формула:
,
къдетоµ- математическо очакване;
(основа на натурален логаритъм);
- Нареченстандартно отклонение.
Следователно този закон се нарича закон за нормалното разпределение, а графиката на функциятаf(x)се наричанормална крива иликрива на Гаус (фиг.6).
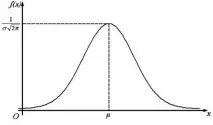
Ориз. 6. Нормална крива на разпределение
Теорема.Математическото очакване на случайна променлива X е приблизително равно на средната аритметична стойност на всички нейни стойности (с достатъчно голям брой опити).
Както може да се види от Фигура 6, графикатана нормалната кривае фигура с форма на камбана, симетрична по отношение на вертикалната линия и асимптотично се доближава до абсцисната ос при .
Основната характеристика на нормалния закон е, че той е ограничаващият закон, към който се приближават други закони на разпределение. При достатъчно голямо население нормалното разпределение се появява и в емпиричното разпределение.
Определение. Съвкупността от всички възможни стойности на случайна променлива и съответните им вероятности образува така нареченототеоретично разпределение.
Определение. Наборът от действителни стойности на случайна променлива, получени в резултат на наблюдения, със съответните честоти (или честоти) образуватемпирично разпределение.
Разгледайте някои свойства на нормалното разпределение.
1. Графиката на нормалното разпределение е дефинирана по цялата осOX, т.е. всяка стойностxсъответства на точно дефинирана стойност на функцията.
2. За всички стойности нах(както положителни, така и отрицателни), функцията приема положителни стойности, т.е. нормалната крива се намира над остаОХ.
3. Границата на функцията с неограничено нарастванеxе равна на нула
.
Тъй като функцията клони към 0 при , оста x е асимптотата на графиката на тази функция.
4. Функцията в точка има максимум, равен на:
.
5. Графиката на криватаf(x) е симетрична спрямо правата, минаваща през точкатах =μ.
Това предполагаравенство за нормално разпределената стойност на режима, медианата и математическото очакване.
6. Коефициентите на изкривяване и ексцес на нормалното разпределение са равни на 0:
= 0;
= 0.
Това предполага значението на изчисляването на тези коефициенти за емпирични серии на разпределение, тъй като те характеризират асимметрията и стръмността на дадения ред в сравнение с нормалния.
7. Промяната на стойностите на параметрите (с непроменени) не влияе на формата на нормалната крива; кривата се измества по остаOxнадясно, ако се увеличава, и наляво, ако намалява.
При промяна на стойностите на параметъра формата на нормалната крива се променя. Максималната ордината на графиката на функцията намалява с увеличаване на стойността (кривата се „свива“ към остаOx) и нараства с намаляване на стойността (кривата се „разтяга“ в положителната посока на остаOy).
На фиг. 7. показва три нормални криви за една и съща стойност и различни стойности на .
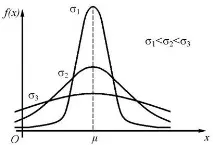
Ориз. 7. Нормални криви за равни и различни
Аналитичен анализ.