Хипотезата на Поанкаре история на проблема, доказателство, значение

В училищния курс всеки е запознат с понятията теореми и хипотези. По правило в живота се засягат най-простите и примитивни закони, докато математиците правят много сложни предположения и поставят интересни проблеми. Далеч не винаги самите те успяват да намерят решения и доказателства, а в някои случаи техните последователи и просто колеги се борят с това от много години.

Институтът Клей през 2000 г. състави списък от 7 така наречени проблеми на хилядолетието, подобен на списъка с хипотези, съставен през 1900 г. Почти всички от тези задачи вече са решени, само една от тях е мигрирала към актуализираната версия. Сега списъкът с проблеми изглежда така:

хипотезата на Ходж;
равенство на класове P и NP;
хипотезата на Поанкаре;
теория на Янг-Милс;
хипотезата на Риман;
съществуване и гладкост на решението на уравненията на Навие-Стокс;
хипотезата на Birch-Swinnerton-Dyer.

Всички те принадлежат към различни дисциплини в математиката и са важни. Например уравненията на Навие-Стокс са свързани с хидродинамиката, но на практика могат да опишат поведението на материята в земната магма или да бъдат полезни при прогнозиране на времето. Но всички тези проблеми все още търсят своето доказателство или опровержение. Освен един.

Теорема на Поанкаре

Да обясните с прости думи какъв е този проблем е доста трудно, но можете да опитате. Представете си сфера, например сапунен мехур. Всички точки от нейната повърхност са на еднакво разстояние от центъра й, който не й принадлежи. Но това е двуизмерно тяло, а хипотезата говори за триизмерно. Вече е невъзможно да си представим, но имаме теоретична математика за това. В същото време, разбира се,всички точки на това тяло също ще бъдат премахнати от центъра.

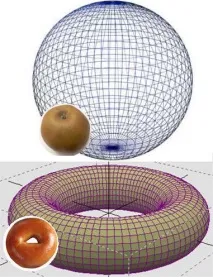
Този проблем принадлежи към топологията - науката за свойствата на геометричните форми. И един от основните термини в него е хомеоморфизмът, тоест висока степен на сходство. За да дадем пример, можем да си представим топка и тор. Една фигура не може да бъде получена от друга по никакъв начин, като се избягват пропуски, но конус, куб или цилиндър от първата ще се получи доста лесно. Тук хипотезата на Поанкаре е посветена на тези метаморфози само с една разлика - говорим за многомерно пространство и тела.

Френският математик Анри Поанкаре работи в различни области на науката. За постиженията му може да се говори например с факта, че съвсем независимо от Алберт Айнщайн той изложи основните положения на специалната теория на относителността. През 1904 г. той повдига проблема за доказване, че всяко триизмерно тяло, което има някои от свойствата на сфера, е тя, с точност до деформация. По-късно тя беше разширена и обобщена, за да се превърне в специален случай на хипотезата на Търстън, формулирана през 1982 г.

Формулировка

Поанкаре първоначално остави следното твърдение: всяко просто свързано компактно триизмерно многообразие без граница е хомеоморфно на триизмерна сфера. По-късно тя е разширена и обобщена. И все пак, дълго време първоначалният проблем създаваше най-много проблеми и беше решен само 100 години след появата му.

Тълкуване и значение

Вече говорихме какво е хомеоморфизъм. Сега си струва да говорим за компактност и просто свързаност. Първото означава само, че колекторът има ограничени размери, не може да се разширява непрекъснато и безкрайно.

По отношение на едносвързаността можем да се опитаме да дадем прост пример. 2Dсфера - ябълка - има едно интересно свойство. Ако вземете обикновена затворена гумена лента и я прикрепите към повърхността, тогава чрез гладка деформация тя може да бъде намалена до една точка. Това е свойството на единичната свързаност, но е доста трудно да се представи във връзка с триизмерното пространство.

Казано съвсем просто, проблемът беше да се докаже, че простото свързване е свойство, уникално за една сфера. И ако, условно казано, експериментът с ластика е завършил с такъв резултат, то тялото е хомеоморфно на него. Що се отнася до приложението на тази теория към живота, Поанкаре вярва, че Вселената в известен смисъл е триизмерна сфера.

Доказателство

Не трябва да се мисли, че от десетките математици, които са работили по целия свят, никой не е мръднал и на йота по този проблем. Напротив, имаше напредък и в крайна сметка той доведе до резултат. Самият Поанкаре не е имал време да завърши работата, но неговите изследвания сериозно напредват в цялата топология.

През 30-те години интересът към хипотезата се завръща. Първо, формулировката беше разширена до "n-мерното пространство", а след това американецът Уайтхед докладва успешно доказателство, по-късно го изостави. През 60-те и 70-те години двама математици наведнъж - Смейл и Столингс - почти едновременно, но по различни начини, разработиха решение за всички n, по-големи от 4.

През 1982 г. е намерено доказателство и за 4, оставяйки само 3. През същата година Търстън формулира хипотезата за геометризиране, като теорията на Поанкаре се превръща в частен случай.

След това работата донякъде замря - американецът Ричард Хамилтън предложи да се използва потокът на Ричи в решението, но се натъкна на трудности и не завърши проучването.

В продължение на 20 години хипотезата на Поанкаре изглеждаше забравена. През 2002 г. бългматематикът Григорий Перелман представи решението в общи линии, като направи някои допълнения шест месеца по-късно. По-късно това доказателство е проверено и доведено „до блясък“ от американски и китайски учени. И самият Перелман изглеждаше загубил всякакъв интерес към проблема, въпреки че реши един по-общ проблем на геометризирането, за който хипотезата на Поанкаре е само частен случай.

Признание и оценки

Разбира се, това веднага се превърна в сензация, защото решението на един от проблемите на хилядолетието просто нямаше как да остане незабелязано. Още по-изненадващ беше фактът, че Григорий Перелман отказа всички награди и награди, като каза, че вече е имал страхотен живот. В съзнанието на жителите на града той веднага стана пример за онзи полу-луд гений, който се интересува само от наука.

Всичко това предизвика много дискусии в пресата и медиите, че популярността на математика започна да го натежава. През лятото на 2014 г. имаше информация, че Перелман е заминал да работи в Швеция, но това се оказа само слух, той все още живее скромно в Санкт Петербург и почти не общува с никого. Сред наградите, които му дават, са не само наградата на института Клей, но и престижният медал на Фийлдс, но той отказва всичко. Въпреки това, Хамилтън, който според Перелман е допринесъл не по-малко за доказателството, също не е забравен. През 2009 и 2011 г. получава и няколко престижни награди и награди.

Отражение в културата

Въпреки факта, че за обикновените хора както твърдението, така и решението на този проблем нямат смисъл, доказателството стана известно доста бързо. През 2008 г. по този повод японският режисьор Масахито Касуга засне документалния филм "Омагьосването на хипотезата на Поанкаре", посветен на един век опити за разрешаване на този проблем.

Участва в заснеманетомного математици, които се занимаваха с този проблем, но главният герой - Григорий Перелман - не искаше да направи това. В снимките са участвали и негови повече или по-малко близки познати. Документалният филм, пуснат на екраните след обществения протест за отказа на учения да приеме наградата, спечели известност в определени кръгове и получи няколко награди. Що се отнася до популярната култура, обикновените хора все още се чудят от какви аргументи се е ръководил петербургският математик, отказвайки да вземе пари, когато може да ги даде, например, за благотворителност.