Избор на вариационни интервали
Сега нашата цел е да изберем две нива за всеки фактор, при които той ще варира в експеримента.
Интервалът на вариация на фактора е определено число (собствено за всеки фактор), добавянето на което към основното ниво дава горното ниво, а изваждането дава долните нива на фактора. С други думи, интервалът на вариация е разстоянието по координатната ос между основното и горното (или долното) ниво. По този начин проблемът за избор на нива се свежда до по-прост проблем за избор на интервал на вариация.
Отбелязваме също, че за да се опрости записването на експерименталните условия и обработката на експерименталните данни, скалите по осите са избрани така, че горното ниво да съответства на +1, долното да съответства на –1, а основното да съответства на нула. За фактори с непрекъсната област това винаги може да се направи с помощта на трансформацията
,
– кодирана стойност на фактора;
– натурална стойност на фактора;
– природна стойност на основно ниво;
– интервал на вариация;
– номер на фактора.
За качествени фактори, които имат две нива, едното ниво се обозначава с +1, а другото -1; редът на нивата няма значение.
Изборът на интервали на вариация е предмет на естествени ограничения отгоре и отдолу. Интервалът на вариация не може да бъде по-малък от грешката, с която експериментаторът фиксира нивото на фактора. В противен случай горното и долното ниво ще бъдат неразличими. От друга страна, интервалът не може да бъде толкова голям, че горните или долните нива да са извън областта на дефиниция. В рамките на тези ограничения обикновено все още има значителна несигурност на избора, която се елиминира с помощта на интуитивни решения.
Моля, имайте предвид, че когато решавате проблемаоптимизация, ние се стремим да изберем за първата серия от експерименти такъв поддомейн, който да направи възможно стъпаловидно движение към оптимума. При проблеми с интерполация интервалът на вариация обхваща цялата описана област.
Изборът на интервали на вариация е трудна задача, тъй като е свързан с неформален етап от планирането на експеримента. Възниква въпросът каква априорна информация може да бъде полезна на този етап? Това е информация за точността, с която експериментаторът фиксира стойностите на факторите, за кривината на повърхността на реакция и за диапазона на параметъра за оптимизация. Обикновено тази информация е ориентировъчна (в някои случаи може просто да е грешна), но е единствената разумна основа, на която да започнете да планирате експеримент. По време на експеримента често се налага да се коригира.
Точността на фиксиране на факторите се определя от точността на инструментите и стабилността на нивото по време на експеримента. За да опростим схемата за вземане на решения, ще въведем приблизителна класификация, като приемем, че има ниска, средна и висока точност. Например, може да се приеме, че поддържането на температурата в реактора с грешка не повече от 1% отговаря на висока точност, не повече от 5% на средна точност и повече от 10% на ниска точност.
Вече споменатите графики на еднофакторни зависимости, както и теоретични съображения могат да служат като източник на информация за кривината на повърхността на реакция. Информация за кривината може да се получи визуално от графиките. Известна представа за кривината се дава чрез анализа на таблични данни, тъй като наличието на кривина съответства на непропорционална промяна в параметъра за оптимизация с равномерна промяна на коефициента. Ще разграничим три случая: функцията на отговор е линейна, функцията на отговор е по същество нелинейна и информацията за кривинатаотсъстващ.
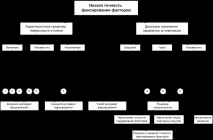
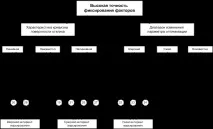
И накрая, полезно е да знаете в какви диапазони се променят стойностите на параметъра за оптимизация в различни точки във факторното пространство. Ако има резултати от определен набор от експерименти, тогава винаги е възможно да се намерят най-големите или най-малките стойности на параметъра за оптимизация. Разликата между тези стойности ще се нарича обхват на параметъра за оптимизация за даден набор от експерименти. Нека се съгласим да правим разлика между широки и тесни диапазони. Диапазонът ще бъде тесен, ако не се различава значително от разпространението на стойностите на параметъра за оптимизация при повтарящи се експерименти (това разпространение определя грешката на експеримента). В противен случай ще считаме диапазона широк. Отчитаме и случая, когато липсва информация. Така че за вземане на решения се използва априорна информация за точността на фиксиране на факторите, кривината на повърхността на реакция и диапазона на параметъра за оптимизация. Всяка комбинация от градации на изброените характеристики определя ситуацията, в която трябва да вземете решение. При приетите градации са възможни 3 3 = 27 различни ситуации. Те са показани на фиг. 3, 4, 5 под формата на кръгове, числата в които съответстват на поредните номера на ситуациите.
Сега сме близо до вземането на решение относно избора на интервали на вариация. Въвеждаме и градация за интервалите. Ще разгледаме широки, средни и тесни интервали на вариация, както и случая, когато е трудно да се вземе недвусмислено решение. Размерът на интервала на вариация е определена част от площта на дефиницията на фактора. Например, можем да се споразумеем за следното: ако интервалът е не повече от 10% от областта на дефиниране, считайте го за тесен, не повече от 30% - за среден, а в други случаи - за широк. Това, разбира се, е много условно и във всеки конкретен проблем трябва конкретно да се дефинират тези понятия, които зависят отне само от размера на областта на дефиниране, но и от естеството на повърхността на реакция и от точността на фиксиране на факторите.
Нека да преминем към разглеждането на блок-схеми за вземане на решения. Първата диаграма (фиг. 3) показва девет ситуации, които възникват с ниска точност на фиксиращите фактори. При избора на решения се взема предвид информацията за кривината на реагиращата повърхност и обхвата на оптимизационния параметър. Типично решение е широк интервал на вариация, тесен интервал на вариация изобщо не се използва, което е съвсем разбираемо при ниска точност.
Средният интервал на вариация в тази схема е избран два пъти, а в деветата ситуация като рядко използвана алтернатива. Тук няма информация за двете функции и изборът на широк интервал изглежда по-естествен.
Най-голямата трудност възниква, когато отговорната повърхност е нелинейна. Има противоречие между ниската точност на фиксиране на факторите и кривината. Първият изисква разширяване на интервала, а вторият - стесняване. Решението се оказва нееднозначно. Как да процедираме? Трябва да се вземат предвид допълнителни препоръки (вижте блок-схемата). На първо място е необходимо да се разбере дали е възможно да се повиши точността на експеримента чрез инженерни решения или чрез увеличаване на броя на повтарящите се експерименти. Ако е възможно, тогава решенията се вземат на базата на блоковата диаграма (фиг. 4) за средната точност на фиксиране на факторите. Ако това не е възможно, тогава няма достатъчно основания за вземане на решение и то става интуитивно.
Тази блокова диаграма, подобно на следващата, служи като много грубо приближение към реалността. На практика има много повече фактори, които трябва да се вземат предвид. Например, решенията, взети за всеки фактор поотделно, се коригират, когато се разглежда съвкупността от фактори.
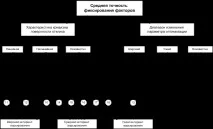
На фиг. 4 показва блокова диаграма за случая на средна точност на фиксиране на коефициента. Характерен е изборът на средния интервал на вариация. Само в случай на нелинейна повърхност и широк диапазон се препоръчва тесен интервал на вариация. Когато се комбинира линейна повърхност с тесен обхват и без информация за обхвата, се избира широк диапазон на вариация. Пунктираната линия, както по-горе, показва рядко използвани алтернативи.
Накрая, на фиг. 5 е построена блокова схема за случай на висока точност на фиксиране на коефициента. Комбинацията от висока точност с нелинейност на повърхността винаги води до избора на тесен интервал. Доста често се избира среден интервал и само в два случая е широк. В последните две блокови диаграми няма двусмислени решения.