Издържайте изпита по математика

Как се издържа изпитът по математика? Въпрос, който няма ясен, еднозначен отговор. Някой иска да вкара само минималния резултат, някой мисли как да се справи с параметрите и задачите по геометрия в трудната част.
Но е безспорно, че е необходимо да се подготвят системно и систематично поне една година, повтаряйки теорията и разработвайки методите за решаване, редовно решавайки задачи по всички теми. Без труд, както се казва - не можете да видите рибата.
В последната статия анализирахме няколко „трудни“ задачи, на които дори добре обучени момчета се спъват поради невнимание. Нека разгледаме нещо друго интересно тук:
27671. Намерете ординатата на пресечната точка на оста y и правата, минаваща през точка B(6;4) и успоредна на правата, минаваща през началото и точката A(6;8).
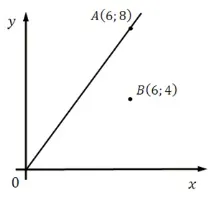
Първият начин (за тези, които обичат да изчисляват и нямат нищо против времето).
Идеята е следната: намираме уравнението на тази линия, след което знаем наклона на линията, можем да напишем уравнението на успоредна линия, минаваща през точка B. След това изчисляваме числото b в уравнението на линията y \u003d bx + b (замествайки координатите на точка B). И едва тогава можем да намерим ординатата, посочена в условието, като заместим абсцисата, равна на нула, в уравнението.
Използваме формулата за уравнението на права линия, минаваща през две точки. Има общ вид:
В нашия случай ще бъде:
Тези точки, през които минава линията, имат координати (0; 0) и (6; 8), което означава:
Нека го приведем във формата y=kx+b:
Тъй като наклоните на успоредните прави са равни, уравнението на правата, минаваща през точка B(6;4), ще бъде както следва:
Намираме стойността на b, като заместваме координатите на точка B (6; 4) в това уравнение:
Така уравнението на права линия ще изглежда така:
Да намерязаместваме ординатата на пресечната точка на тази линия с оста y в намереното уравнение за абсцисата x \u003d 0:
*Втори метод (без изчисления).
Според координатите на листа в клетка изграждаме скица:
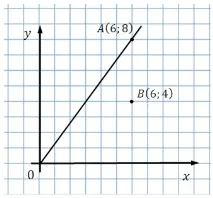
Чрез паралелен превод преместваме правата линия надолу по оста y до точката (6; 4):
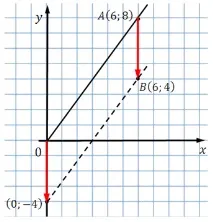
Смяната е 4 бр. Тоест точка A(6;8) "премина" до точка B(6;4), а точка O(0;0) "премина" до точка (0;–4).
По този начин успоредна права линия, минаваща през точка B(6;4), ще пресече оста y в точка (0;–4). Желаната ордината е -4.
*Тази задача и други с координатна равнина са изключени от отворената банка задачи към момента на писане на тази статия. На уебсайта на Дмитрий Гушчин те са достъпни. Ще вземат ли изпита? не знам Но реших да публикувам решението, ще бъде полезно във всеки случай.
Ако обичате да решавате такива задачи алгебрично, давайте. Но е по-добре да не губите време и да използвате втория подход. Работи и в много други подобни задачи. Опитното око дори не трябва да изгражда скица (на лист в клетка), отговорът идва след 5 секунди. И няма значение през кои точки минава линията, основното е да я преместите правилно (прехвърляне).
99610. По море два сухотоварни кораба следват паралелни курсове в една посока: първият е дълъг 120 метра, вторият е дълъг 80 метра. Първо, вторият кораб за насипни товари изостава от първия и в даден момент разстоянието от кърмата на първия кораб за насипни товари до носа на втория е 400 метра. 12 минути след това първият кораб за насипни товари изостава от втория, така че разстоянието от кърмата на втория кораб за насипни товари до носа на първия е 600 метра. С колко километра в час скоростта на първия товарен кораб е по-малка от скоростта на втория?
*Препоръка! Когато решавате такива проблеми, не забравяйте да направите скица и да обозначите известноразмер, яснотата помага много.
Не забравяйте да конвертирате всички дължини в километри.
Веднага обърнете внимание на факта, че в условието не е дадена скорост. Да ги обозначим. Нека скоростта на първия кораб за насипни товари е x (km/h), на втория y (km/h).
Времето, за което са се движили сухотоварните кораби, е същото - 12 минути.
Преобразувайте минути в часове: 12 минути са 1/5 от час или 0,2.
Нека направим таблица и попълним колоната "разстояние":
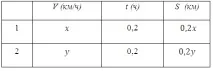
Отбелязваме на скицата дължината на сухотоварните кораби, разстоянието между тях, както и разстоянието, което е изминал първият, то е равно на 0,2x km:
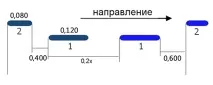
*Тъмен цвят показва началната позиция, син - крайната позиция.
Изчислете от скицата разстоянието, което вторият ще измине напред. Ще изчислим от кърмата (отзад), метрите са преобразувани в километри:
Сега можем да приравним стойността на таблицата и получената стойност (което означава разстоянието, изминато от секундата):
Както можете да видите, в тази задача изобщо не е необходимо да намирате самите скорости, достатъчно е да намерите разликата им и отговорът е готов.
Нека използваме следния подход. Възможно е да се опрости условието и да се приеме скоростта на първия кораб за насипни товари като 0 km/h (той стои неподвижен), да се означи скоростта на втория с произволна променлива, да се остави y. Нека изградим скица:
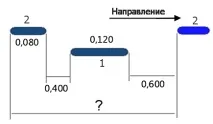
Оказва се, че вторият е минал покрай първия и е надвил:
Скоростта на втория, както вече беше споменато, е y. Тоест за 0,2 часа е изминал 0,2 км. Можем да напишем:
Изчисляваме разликата в скоростта:
* Вторият подход донякъде опростява решението и задачата на пръв поглед "грозна" става проста. Има и момчета, които могат да смятат устно.
26720. Намерете най-голямата стойност на функция
1. e \u003d 2,7182818 .... (безкраен десетичен знак).
2. Натурален логаритъм е логаритъма, в основата на който еномер e.
Намерете производната на дадената функция:
Намерете нулите на производната на даден интервал:
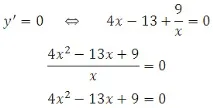
Чрез решаване на квадратното уравнение получаваме:
Точката x=1 принадлежи на дадения сегмент и го разделя на интервали, точката x=9/4 не му принадлежи.
Нека определим знаците на производната на интервалите:
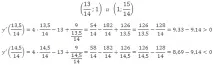
*Грешка! Трябва да отделите време за разделяне.
Нека опишем поведението на функцията:
В точката x=1 знакът на производната се променя от положителен на отрицателен, което означава, че това е максималната точка. Изчисляваме стойността на функцията:
Сега нека помислим логично. Ако вземем предвид, че отговорът трябва да е цяло число или последна десетична дроб, тогава числото 1 трябва да стои под знака на логаритъма, в противен случай (когато x ≠ 1) няма да можем да изчислим стойността на логаритъма, за да получим посочената стойност в отговора. Единицата е включена в сегмента (1 е 14/14). Така се оказва, че в точката x \u003d 1 стойността на функцията ще бъде най-голямата. Ние го изчисляваме:
Можете също да направите следното. Да се изчисли стойността на функцията в три точки - в точката x=1 и в границите на отсечката:
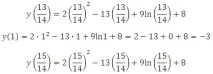
*В случаите, когато има дроби под знака на логаритъма, в резултат няма да получим цяло число или крайна десетична дроб. Отговорът е очевиден, той е -3.
*Както можете да видите, първият подход отнема много време, а вторият начин проблемът може да бъде решен за почти минута.
282861 Намерете най-малката стойност на функция
Тъй като интервалът е малък, можете да направите без изчисляване на производната и решаване на задачата, като използвате стандартния алгоритъм.
Заместете целочислените стойности от сегмента -4; -3; -2 и -1 във функцията и изчислете:
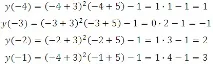
Най-малката стойност на функцията е -1.
Ако още не знаете, тези задачи са включени вКнигата "Най-трудните задачи на изпита по математика." Те са общо 188, ще има допълнения в бъдеще.