Изпит Решаване на нелинейни уравнения

Отделете корените на уравнението

графично и прецизирайте един от тях:

• метод на разделяне на половина;
• метод на проста итерация;

с точност ε=0.001.

Създайте функции, които изпълняват посочените методи, изградете графична илюстрация на методите, проверете резултатите с помощта на вградени функции, оценете точността на получените стойности.

Методът на разполовяване или методът за разделяне на сегмент наполовина е най-простият числен метод за решаване на нелинейни уравнения от вида F(x)=0. Приема се само непрекъснатостта на функцията F(x).

Графично представяне на метода на разполовяването

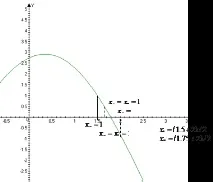
Нека решим задачата в пакета Matkad:

Идеята на метода е да се изгради права линия (т.е. хорда, свързваща две точки от графиката) с помощта на две точки и да се вземе като следващо приближение абсцисата на пресечната точка на тази права с остаOx.

Графично представяне на метода на акордите

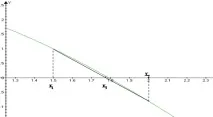
Нека решим задачата в пакета Matkad:

3. Тангентен метод (Нютон)

Графично представяне на метода на допирателната

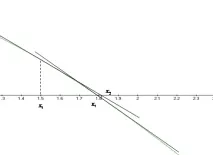
Нека решим задачата в пакета Matkad:

4. Методът на секанса

Графично представяне на метода на секущата

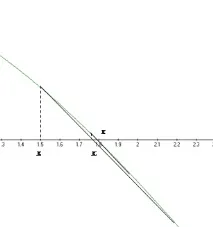
Нека решим задачата в пакета Matkad:

5. Метод на проста итерация

Графично представяне на простия итерационен метод

Нека решим задачата в пакета Matkad:

Решете задачата на Коши за диференциалното уравнение на интервала [a,b] с първоначално зададено условие и стъпка на интегриране h:

1. Метод на Ойлер;

2. Метод на Runge-Kutta от 4-ти ред на точност.

3. проверете решението с вграденифункции на пакета MathCAD.

В решението оставете 5 цифри след десетичната запетая.

Нека решим задачата в пакета Matkad:

2. Метод на Runge-Kutta от 4-ти ред на точност

Нека проверим решението с помощта на вградените функции на пакетаMathCAD

---