ИЗПОЛЗВАНЕ НА ЦВЕТНИ ЧЕРТЕЖИ ПРИ ПРОЕКТИРАНЕ НА ПОВЪРХНОСТИ В ОПИСАТЕЛНА ГЕОМЕТРИЯ -

ИЗПОЛЗВАЙТЕ ЦВЕТНИ СНИМКИ

ПО ВРЕМЕ НА ДИЗАЙН НА ПОВЪРХНОСТТА

В ОПИСАТЕЛНА ГЕОМЕТРИЯ

Vertinskaya N.D. професор, доктор на техническите науки

Иркутски държавен технически университет, България

Както е известно, повърхносттае двупараметърно множество от точки [1].

Например една равнина носи набор от точки, които имат две координати.

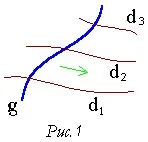
Повърхнина може да се образува чрез преместване на правата gi по някаква права di. Този начин на формиране на повърхността се наричакинематичен. Линията gi се наричагенерираща, линията di-направляваща(фиг.1). Говорейки за кинематичния метод на образуване на повърхността, се въвежда понятиетодетерминантана повърхността,като набор от независими условия, които еднозначно определят повърхността.

Детерминантата на повърхността се състои от две части:геометричнаиалгоритмична.Например сферата F се определя еднозначно от центъра и радиуса, който се записва - Ф(О,R). Центърът O и радиусът съставляват геометричната част на детерминантата, а алгоритмичната част е формулирана със следните думи: сферата е набор от точки в пространството, отдалечени от точката O на разстояние R.

Повърхности като фюзелажи на самолети, каросерии на автомобили, турбинни перки и др. имат сложни закони на образованието. Техните оп-детерминанти са сложни и разнообразни. Затова беше разработен универсален детерминант, чиято геометрична част е дискретна рамка (набор) от генератори, а алгоритмичната част е алгоритъмът за уплътняване на рамка (преход от дискретна рамка към непрекъсната).

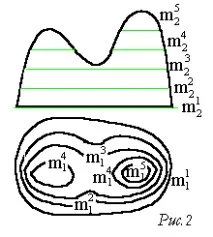
Например, в топографията, релефът на земната повърхност се определя от семейство контурни линии - участъци от повърхността чрез равнини на нивото (фиг. 2).

Изграждането на проекционни изображения на повърхности причинява определени трудности. Следователно кинематичните повърхнини се задават от проекциите на елементите на геометричната част на определителя. За да определим една повърхност, която сме дали, или семейство от повърхности, трябва да разберем дали чертежът на повърхността е пълен. Критерият за пълнота на чертежа е: по една проекция на точка може ли да се построи нейната единствена втора проекция.

Някои повърхности могат да бъдат описани с алгебрични уравнения в декартова правоъгълна координатна система. В този случай повърхността ще бъдеалгебрична, в противен случай ще бъдетрансцендентална.

Редът на една повърхност се определя от броя точки на нейното пресичане с която и да е права.Това е определение за алгебрични повърхности, но ако има безкрайно много точки на пресичане на една повърхност с права, тогава такава повърхност е трансцендентална.

Редът на повърхността също се определя от реда на равнинната крива, получена при пресичането на повърхността с която и да е равнина.

Разнообразието от повърхности изисква тяхното систематизиране. При разглеждане на кинематичния метод на формиране на повърхността систематизацията се основава на две характеристики: вида на генераторите и закона за тяхното изместване.

Според формата на образуващата всички повърхности могат да бъдат разделени налинейчати(пораждаща линия) инелинейчати(пораждащата крива е пространствена или плоска), а според закона за изместване на образуващата - повърхности на паралелно пренасяне, въртене и спирални.

Повърхнините, образувани от движението на права линия по даден закон, се наричат линейка. Линейчатите повърхности се използват широко в инженерството. Това са покрития и огради на архитектурни конструкции, повърхности на крила и оперение, отделения на фюзелажа, пилони на самолети, повърхностицилиндрични и конусни зъбни колела и др. Законът за движение на права линия обикновено се дава от водачите. Не може да има повече от три такива водача.

Наистина, нека са дадени три водещи пространствени криви

(фиг. 3).

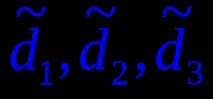
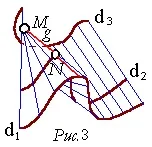
Да вземем например точката МО

и да я вземем за върха на коничната повърхнина S(М,

), в която кривата

ще бъде водеща, тогава кривата

ще пресича коничната повърхнина S (M,

) поне в една точка, например N. Правата линия (МN)=g МС задължително ще пресича кривата

поне в една точка, например, L. по кривата

получаваме набор от прави линии, които избират в пространството единствената линейчата повърхност F. Една от посоките

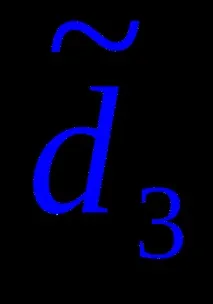
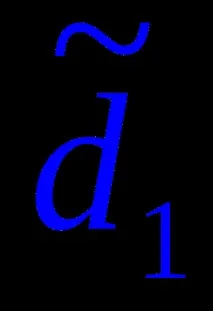
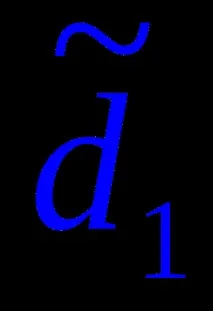
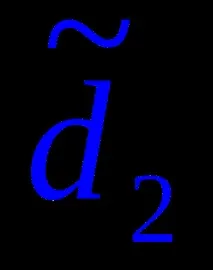
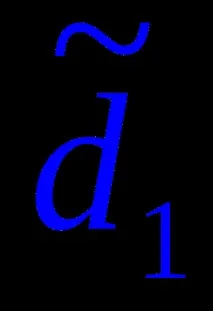
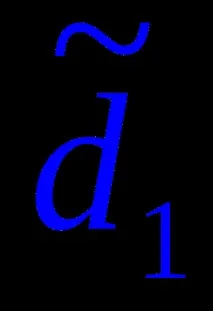
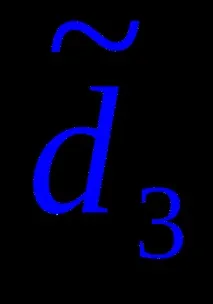
криви, например,

могат да бъдат заменени с повърхност (равнина) .

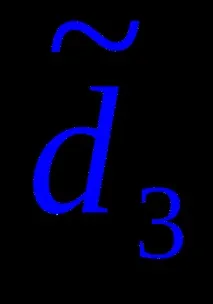
Тогава линейчатата повърхност ще се нарича каталунска повърхност.

Образуващите g на тази повърхност отговарят на три условия: те пресичат кривите

и са успоредни на повърхността (равнината)  Ако изберем равнина като повърхност D, тогава получените повърхности ще се наричат повърхности с равнина на паралелност.

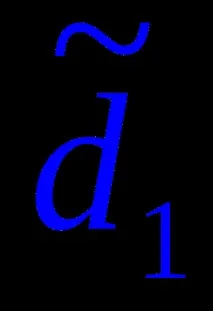
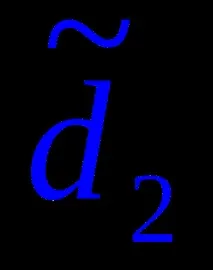
В зависимост от вида на водачите

линейни повърхности с

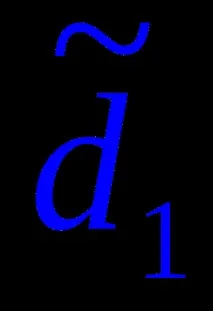
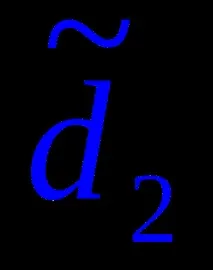
равнина на успоредностсе наричат цилиндроид, коноид и наклонен

Повърхности с успоредна равнина

Цилиндроиде линейчата повърхност с равнина на успоредност, в която водачите

са пространствени или равнинни криви.

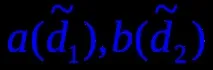
За решаване на задачи върху повърхността на цилиндроид е необходимо да се зададе рамката му с праволинейни генератори gi(gi1, gi2). Нека имаме равнина на успоредност P1, така че gi ще бъде хоризонтална. След това изграждаме няколко праволинейни генератора.

За даза да сме сигурни, че сме задали единствената повърхност на цилиндроида, трябва да решим задачата върху нейната повърхност (фиг. 4):

ако точка от повърхността е дадена от едната си проекция, тогава е необходимо да се намери втората й проекция, ако е уникална, тогава получената повърхност ще бъде уникална.

Решение. Нека точката A е дадена и зададена от фронталната проекция A2, след което начертаваме през нея хоризонталната проекция на линейната образуваща`g2 и използвайки нея ще построим хоризонтална проекция`g1, върху която ще проектираме точката A2

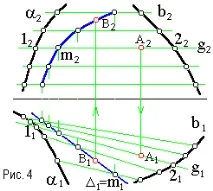
и вземете точка A1. Ако точка B е дадена от нейната хоризонтална проекция B1, тогава, за да се намери фронталната проекция B2, е необходимо да се начертае хоризонтално през

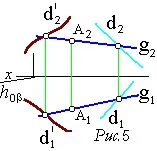
проектираща равнина, например

, където

е кривата, по която пресича равнината

с цилиндър-оида. Построявайки фронталната проекция на кривата

и проектирайки точка B2, върху

получаваме проекцията B1. Оттук заключаваме, че повърхността на цилиндроида е уникална.

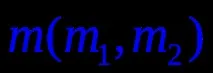
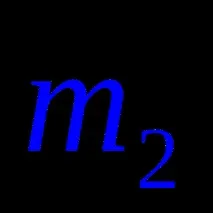
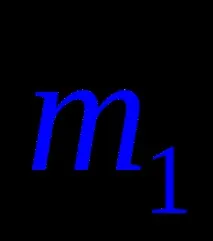
Коноидае линейчата повърхност с равнина на успоредност, имаща криволинейни и праволинейни водачи. гео-

метричната част на детерминантата ще изглежда така

поставете така: Ф(

, ` d ” ) (фиг. 5).

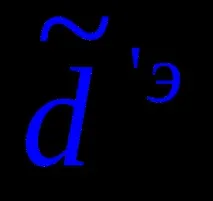
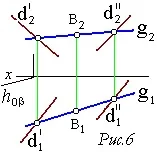
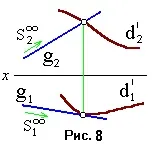
Наклонена равнинае линейчата повърхност с равнина на успоредност и праволинейни образуващи ` d ’ , ` d ” (фиг. 6).

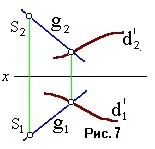
Конична повърхностс обща форма се формира от движението на права линия g (генерираща), минаваща през фиксирана точка S (върх) и пресичаща водещата крива d’ (фиг. 7).

онична повърхност с неправилен връх S ¥ (s) се наричацилиндрична(фиг. 8).

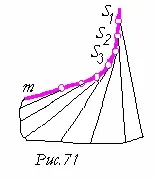
Линейчатата повърхност, образувана от набора от допирателни към пространствената крива m, се наричаторзалнаилиповърхност с обратен ръб. Водещата крива m на повърхността Ф се наричавъзвратен ръб(фиг. 9).

Повърхността, образувана от въртенето на определена права (генерираща) около определена права линия i, се наричаповърхност на въртенеГеометричната част на такава повърхност се записва по следния начин: Ф (i, g). На чертежа повърхността на въртене Ф (i, g) е дадена от оста i и образуващата g (фиг. 10).

За да се построи точка AÎF, е необходимо да се определи окръжността на m-сечението на повърхнината Ф с равнината S2^i. Окръжността m се определя от центъра

О(О1,О2)=iÇS и радиус [OL], където L= lÇS.

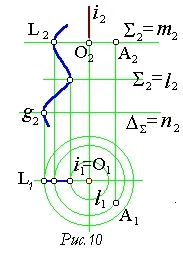
Сеченията на повърхността Ф с равнини, перпендикулярни на оста i, се наричат паралели.

Паралел, чийто радиус е по-голям от радиуса на съседните паралели, се наричаекваторn (n1, n2). Паралел, чийто радиус е по-малък от съседните радиуси, се наричагърлоl (l1, l2).

Участъци от повърхността на въртене от равнини, минаващи през нейната ос, се наричат меридиани.Меридианът, принадлежащ към фронталната равнина на нивото Г1=g1, се наричаглавен меридианg (g1, g 2).

Семействата от паралели и меридиани образуват правоъгълна мрежеста рамка на повърхността на въртене. През всяка точка от повърхността има един паралел и един меридиан, пресичащи се под прав ъгъл.

След това разгледайте повърхностите на въртене от четвърти ред, получени чрез въртене на окръжността g около оста i, която лежи в равнината на окръжността, които се наричат тори. В зависимост от местоположението на i-оста спрямо центъра на окръжността, торът може да бъде отворен (d > r) или затворен (d