KNOU INTUIT, Лекция, Методи за клъстерен анализ

При голям брой наблюдения йерархичните методи за клъстерен анализ не са подходящи. В такива случаи се използват нейерархични методи, базирани на разделяне, които са итеративни методи за разделяне на първоначалната популация. По време на процеса на разделяне се формират нови клъстери, докато се изпълни правилото за спиране.

Такова нейерархично групиране се състои от разделяне на набор от данни на определен брой отделни клъстери. Има два подхода. Първият е да се определят границите на клъстерите като най-плътните области в многомерното пространство на първоначалните данни, т.е. дефиниция на клъстер, където има голяма "концентрация на точки". Вторият подход е да се минимизира мярката на разликата в обекта

Алгоритъм k-средни (k-средни)

Най-често срещаният сред нейерархичните методи е алгоритъмът на k-средните стойности, наричан ощебърз клъстерен анализ. Пълно описание на алгоритъма може да се намери в Hartigan and Wong (1978). За разлика от йерархичните методи, които не изискват предварителни предположения за броя на клъстерите, за да може да се използва този метод, е необходимо да има хипотеза за най-вероятния брой на клъстерите.

Алгоритъмът за k-средни стойности изгражда k клъстера, разположени на възможно най-голямо разстояние един от друг. Основният тип проблеми, които решава алгоритъмът на k-средните, е наличието на предположения (хипотези) относно броя на клъстерите, като същевременно те трябва да бъдат възможно най-различни. Изборът на числото k може да се основава на предишни изследвания, теоретични съображения или интуиция.

Обща идея на алгоритъма: даден фиксиран брой k клъстери за наблюдениесе сравняват с клъстери, така че средните стойности в клъстера (за всички променливи) да се различават възможно най-много една от друга.

Описание на алгоритъма

Първоначално разпределение на обектите по клъстери.

Избира се числото k и на първата стъпка тези точки се считат за "центрове" на клъстерите. Всеки клъстер съответства на един център.

Изборът на начални центроиди може да се извърши, както следва:

избор на k-наблюдения за максимизиране на първоначалното разстояние;
случаен избор на k-наблюдения;
избор на първите k-наблюдения.

В резултат на това всеки обект се присвоява на конкретен клъстер.

Изчисляват се центровете на клъстерите, които след това и по-нататък се считат за средни координати на клъстерите. Обектите се преразпределят отново.

Процесът на изчисляване на центрове и преразпределение на обекти продължава, докато не бъде изпълнено едно от следните условия:

клъстерните центрове са се стабилизирали, т.е. всички наблюдения принадлежат към клъстера, към който са принадлежали преди текущата итерация;
броят на итерациите е равен на максималния брой итерации.

На фиг. Фигура 14.1 показва пример за това как работи алгоритъмът на k-средните за k равно на две.

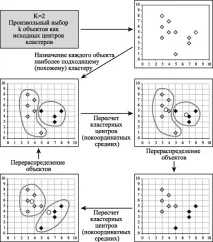
Изборът на броя на клъстерите е сложен въпрос. Ако няма предположения за това число, се препоръчва да се създадат 2 клъстера, след това 3, 4, 5 и т.н., като се сравняват резултатите.

Проверка на качеството на групиране

След получаване на резултатите от клъстерния анализ с помощта на метода k-средни стойности, трябва да се провери правилността на клъстерирането (т.е. да се оцени как клъстерите се различават един от друг). За да направите това, се изчисляват средните стойности за всеки клъстер. Доброто групиране трябва да доведе до много различни средства за всички измервания или понеповечето от тях.