КВАДРАТУРА НА КРЪГА
Чудеса и приключения11/95
КВАДРАТУРА НА КРЪГ, НЕ Е МАТЕМАТИЧЕСКА ЗАДАЧА!
ЧРЕЗ НЕЯ ЧОВЕЧЕСТВОТО СЕ СВЪРЗВА С КОСМИЧЕСКИЯ РАЗУМ.
В живота се случва така, че на пръв поглед напълно несвързани явления и неща изведнъж се оказват в някаква кореспонденция помежду си. Някъде прочетох, че тези, които имат способността да откриват или намират такива връзки, са гениални хора.
През годините срещнах доста необичайни знаещи хора, но един от тях - Александър Константинович Абрамов (1906-1980) - беше за мен човек, разбира се, гений. Полковник от авиацията и специалист по въздушна фотография, той е в същото време любител египтолог, който посвещава цялото си свободно време на мистериите на египетските пирамиди: математически, астрономически и исторически.
Той беше сигурен, че много информация от древната математика и архитектура, египетски и гръцки паметници на културата са дошли до нас от космоса. Но от всички мистерии на математиката на древния свят той се интересуваше най-много от решаването на квадратурата на окръжност, тоест построяването на квадрат, равен на окръжност, с помощта на пергел и линийка.
Съвременната наука смята тези проблеми по принцип за неразрешими, въпреки факта, че има легенди, според които математиците от древността, и по-специално питагорейците, са знаели тяхното решение, но са го пазили в тайна, тъй като е пряко свързано с архитектурата.
Веднага трябва да предупредя читателя, че не съм виждал работата на Абрамов за квадратура на кръга, поне в нейния бял окончателен вариант. Тази история е опит да възстановя това произведение според откъслечните си спомени. Затова, ако някой от читателите, които са по-запознати с творбатаподробно (и това е възможно, тъй като Абрамов имаше доста широк кръг от познати), не е съгласен с някои места от моята интерпретация на проблема, тогава нека приеме тази забележка като извинение за твърде свободния стил на представяне, въпреки че, струва ми се, в основните идеи на Абрамов съм хванал правилно.
Основната идея на Абрамов при решаването на квадратурата на окръжността беше убеждението, че съвременната математика не разглежда този проблем съвсем правилно. Официалната наука смята, че решаването на проблема с квадратурата на окръжност, тоест определянето на площта на квадрат, равен на окръжност, чрез конструкцията е принципно невъзможно. За такава конструкция е необходимо да се определи числото n, а според науката то е трансцендентно число и следователно фундаментално не се поддава на дефиниране чрез конструиране или, с други думи, на дефиниране по геометричен начин. Числото p се разбира като съотношение на обиколката към диаметъра и по целия свят се смята, че обиколката съдържа три диаметъра с малък остатък, изразен чрез безкрайна дроб, тоест с безкраен брой цифри след десетичната запетая: "Пи" - числото = 3,1415926. и т.н.
Според Абрамов, който е заимствал тази идея от древните египтяни и питагорейците, числото "пи" изобщо не е трансцендентно число, а е равно на дробта 22/7. И тяхното знание, той винаги подчертаваше и го показваше на базата на моделите, заложени в архитектурата на пирамидите, идваше от Космоса. Това означава, че за практически цели числото n се определя от стойността 22/7, т.е. ако разделим диаметъра на кръг на 7 равни части, тогава самият кръг ще съдържа 22 такива части и тази стойност вече може да бъде определена геометрично. Не съм съгласен с официалната наука с такова определение на числото, но всеки човек, дори с молив и хартия, можеопредели, че числото 22/7 = 3,1428571. и, следователно, разликата между тази стойност и "официалното" число l е само 0,0013. И тази точност, много по-малка от един процент, напълно отговаря на всички изисквания на практиката, особено след като е просто невъзможно да се постигне по-голяма точност с компас и линийка.
Предположението на Абрамов, че числото tt е част от 22/7, позволява бързо и лесно определяне на квадратурата с помощта на пергел и линейка. Първо, помислете за известния "египетски" правоъгълен триъгълник, наречен "кралски". В него краката и хипотенузите съдържат съответно 3, 4 и 5 единици дължина. Особеността на такъв триъгълник е, че той е единствен по рода си: няма друг триъгълник с различно съотношение на страните, чиято хипотенуза и крака биха били съизмерими един с друг.
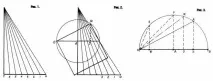
Египтяните, според Абрамов, не биха могли да знаят това според тяхното научно ниво, но те са използвали точно този триъгълник, защото им е даден. Но този триъгълник е забележителен не само със съотношението си. Чрез него, смята Абрамов, египтяните определят квадратурата на кръга. Разгънете този триъгълник в права линия, както е показано на фиг. 1, а отсечката CB съдържа 3 единици, AC - 4 и AB - 5. От центъра в точка A начертайте окръжност с пергел с радиус AB, равен на 7 единици. Нека начертаем диаметъра на окръжността OB по сегмента BB1, който ще бъде равен на 14 части. След това от точка C възстановяваме перпендикуляра до пресечната точка с окръжността - SD. Тогава сегментът OS, взет като страна на квадрата, образува площ, равна на площта на дадения кръг - т.е. проблемът с квадратурата е решен (макар и с точност 22/7 и, както казах, тази точност е много по-висока от един процент).
Нека напомня на читателя, че всички точки A, B и C принадлежат на царскататриъгълник. Но ако пренебрегнем египетския триъгълник, тогава задачата се свежда до разделянето на радиуса на окръжността на 7 равни части. За практически цели това е много лесно да се направи. Ето един начин. Ние правим шаблон от прозрачна хартия, както е показано на фиг. 2. Освен това трябва да се има предвид, че основата на шаблона трябва да бъде успоредна на този сегмент. Нека вземем произволна окръжност (фиг. 3), начертаем в нея диаметър и върху него сложим шаблон, така че да разделим радиуса на 7 части. И от края на третата част изчертаваме перпендикуляр на диаметъра, докато се пресече с кръга в точка D. Сегментът DO е страната на желания квадрат. Самият читател може да провери правилността на тези конструкции, за които ще му трябват знания само в обема на средното училище.
Удивително е, каза Абрамов, как древните египтяни са решавали толкова сложни проблеми чрез елементарни конструкции. Самите те не можаха да стигнат до това, но широко използваха тези методи, но ги използваха механично, без да разбират. Това може да е само в един случай: ако са го получили отвън. Но числото p има не само утилитарен смисъл, тъй като съотношението на обиколката към диаметъра е важно не само за ежедневието. Целият свят и цялата Вселена от атома до планетите се движи по кръгови или близки до кръгови орбити, следователно числото има и космическо значение.
Нека се върнем отново към пи. Според Абрамов дробта 22/7 също е числено равна на дробта 3 1/7. В тази дроб има три числа: три, едно и седем. Извинете, но тази комбинация от числа вече сме я срещали някъде. Да, Пушкин в известната си "Дама пика": три, седем. асо (асо на карти преди и дори сега винаги се означаваше с една икона, следователно асото може да се счита за единица).
Между другото, дробите от този набор от числа също са интересни:1 3/7, умножено по 7, дава свещеното число на Питагор – 10, а дробта 7 1/3, умножена по 3, дава числото 22, тоест отново разкрива връзка с числото n.
Но обратно към Пиковата дама. И така, тройка, седем, асо. Самият Пушкин е свързан по непонятен начин с тези числа. Да вземем например годината на смъртта му 1837 г. Да си припомним, че съвременната хронология е въведена от Петър I през 1700 г., до което годините в Русия се броят от митичната дата на сътворението на света. Ако извадите 1700 от 1837, ще получите точно 137 години.
Е, как самата „Дама пика“ има, така да се каже, лични отношения с тройката, седмицата и асото? Според легендата картите се появяват в ранното средновековие заедно с номадските цигани. А историческите карти за игра, повече или по-малко близки до нашите, стават известни около 1415 г. във френския двор, откъдето влизат в играта. Обикновено картата, съответстваща на текущата дама пика, беше изобразена като богинята на мъдростта - Атина Палада. Един от нейните свещени или сакрални атрибути е копие в ръката или щука, откъдето идва и името - дама пика. Но мъдростта на гръцки е София и според историята на църквата римска аристократка на име София, заедно с нейните дъщери: Вяра, Надежда и Любов, са получили мъченически венец в Рим през 137 г. при император Адриан. Мощите на светите мъченици са изпратени от папа Адриан през 777 г. (три седми) на епископ Ремигий от Страсбург в Елзас, в град Ехо, където техният каменен ковчег е показан в църквата. През 1037 г. в Киев княз Ярослав Мъдри (т.е. по някакъв начин свързан с мъдростта - София) основава катедралата Св. София. През 1073 г. е съставен първият български летопис, в който за първи път се споменава за призоваването на варяжките князе да управляват Русия. Императрица Екатерина Велика е родена през 1730 г. Съвременниците често в поетичните ипроизведения на изкуството й придават атрибута на богинята на мъдростта – Атина.
Освен тези факти има и други интересни данни. 1307 г. - поражението на рицарите тамплиери във Франция. През тази година Данте започва да пише своята Комедия. В Швейцария Вилхелм Тел събаря със стрела ябълка от главата на сина си по заповед на вицекраля император Геслер и поставя началото на първата в света победоносна буржоазна революция в Европа. През 1703 г. Петър I основава Санкт Петербург върху финландските блата.
И така, богинята на мъдростта София и световната константа Щ са свързани по непонятен начин и това е естествено, смята А. Абрамов, защото целият свят, включително и ние, сме деца на един Космос.