ЛЕКЦИИ THEORMEX - Lek14D(prez)
ДИФЕРЕНЦИАЛНИ УРАВНЕНИЯ НА ДВИЖЕНИЕТО НА МЕХАНИЧНАТА СИСТЕМА В ОБОБЩЕНИТЕ КООРДИНАТИ
Уравнения на Лагранж от 2-ри род
1. Уравнения на Лагранж от 2-ри род
Общото уравнение на динамиката в обобщени координати е следното:
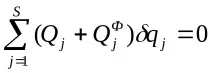
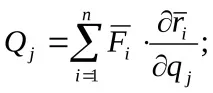
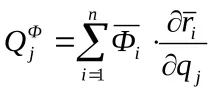
Избираме обобщените координати
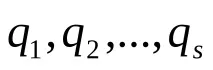
(14.2)
за всички .
Като се има предвид това
Радиус векторът на точкатаMiсъщо е функция на обобщени координати и време
(14.3)
Тъй като обобщените координати на системата
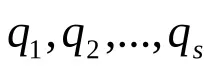
(А)
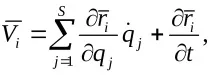
а при стационарните връзки
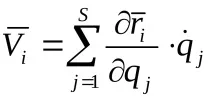
Тук производните на обобщените координати по отношение на времето
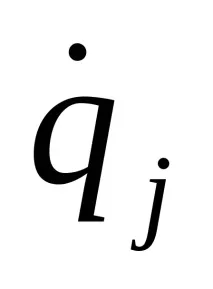
От израз (а) следва, че частната производна на Viпо отношение на всяка обобщена скорост
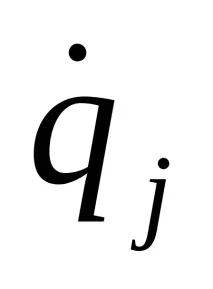
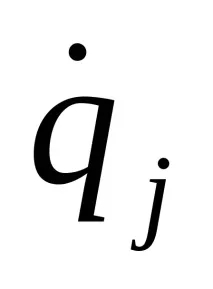
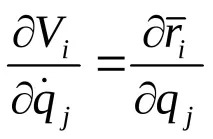
Кинетичната енергия на механична система се определя по формулата
(14.6)
От израза (14.4) следва
Нека намерим частните производни на кинетичната енергия по отношение на обобщената координата

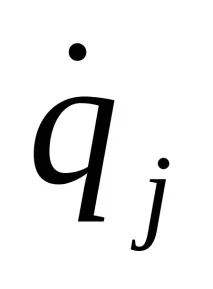
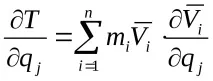
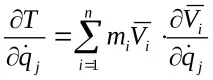
Преобразуваме последния израз въз основа на равенство (b)
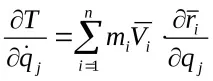
Разграничете този израз по отношение на времето
(V)
Разгледайте двете суми от дясната страна на равенството (c).
За несвободна материална точка
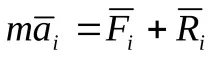
1. Въз основа на израза за обобщената сила намираме:
2. За да установите стойността на втората сума, разгледайте израза
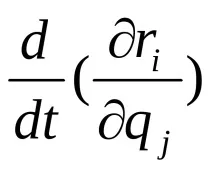
(G)
Нека намерим частната производна (
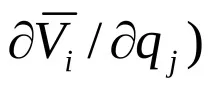

д)
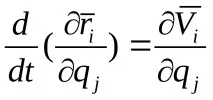
Използвайки тази зависимост, трансформираме втората сума от дясната страна на равенството (c)

Заместваме намерените стойности на двете суми в равенство (c) и разглеждаме механична система със стационарни идеални ограничения, за които
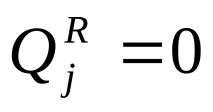
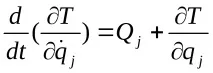
(14.7)
при използване на уравнения на Лагранж от втори род:
Определете броя на степените на свобода на системата и изберете най-удобните обобщени координати;
Изчислява кинетичната енергия на системата и я изразява чрез обобщени координати и обобщени скорости;
Изчислява производни на кинетичната енергия;
Определяне на обобщените сили, съответстващи на избраните обобщени координати;
Заместете всички изчислени количества в уравненията на Лагранж и определете желаната стойност (най-често това е ускорение).
За да съставим лявата страна на тези уравнения, кинетичната енергия трябва да бъде изразена чрез обобщени координати и обобщени скорости.
Обобщените сили могат да бъдат намерени или директно, чрез проекции върху осите на декартовите координати (уравнение (13.6)),
или като координати за вариации на обобщени координати в израза за възможна работа (уравнение (13.4)).
2. Кинетичен потенциал
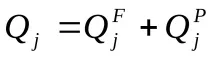
Ако разглежданата система подлежи насамо консервативни сили, тогава обобщената сила се определя от
В този случай уравненията на Лагранж от втори род приемат следната форма
И
Следователно кинетичният потенциалLе функция на обобщени координати, обобщени скорости и време
Потенциалната енергия е функция само на обобщени координати и време, така че
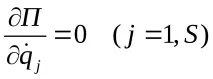
Използвайки това условие, получаваме
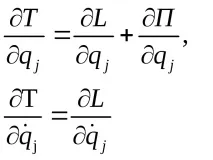
Замествайки тези частни производни в уравненията на Лагранж, получаваме
(14.8)
Уравнения (14.8) се наричат уравнения на Лагранж от втори род за консервативна система.
3. Циклични координати
Обобщените координати, които не са изрично включени в израза на кинетичния потенциалLсе наричат циклични координати.
Да предположим, че средSобобщените координатни системи, координатните системи са циклични.
Тогава, по дефиниция на цикличните координати, производните на кинетичния потенциал по отношение на тези координати са равни на нула:
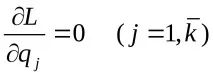
В този случайkуравненията (14.9) приемат формата
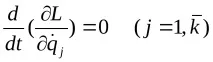
Тези уравнения се наричат циклични интеграли.
1) Позицията на точка в пространството се определя от три координати. Нека вземем декартовите координати като обобщени. Тогава
Кинетичен потенциал на точка
Координатитеx,yне са включени в израза на кинетичния потенциалL, тоест те са циклични координати. Цикличните интеграли имат формата
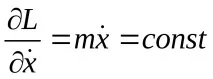
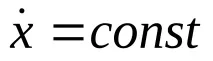
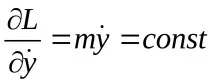
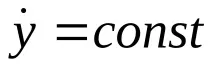
Тези изрази показват, че проекциите на скоростта на точката върху хоризонталните координатни оси са постоянни, т.е. само вертикалната компонента на скоростта на точката се променя под действието на гравитацията.