Някои въпроси по геометрията на изродените триъгълници
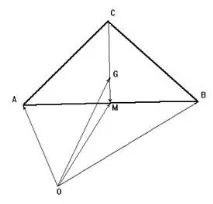
Фигура 1. Центроид на триъгълник
Използването на методите на векторната алгебра позволява да се разкрият онези специални свойства на фигурите, които могат да ни убегнат по време на визуално-геометричното им разглеждане, и в същото време да не загубим геометричната видимост на изучавания факт (както често се случва при използването на метода на координатите).
Нека се спрем на някои факти, свързани с геометрията на триъгълника, които по-късно ще бъдат приложени към изродени триъгълници, което ще ни позволи да получим интересни резултати.
Нека се споразумеем за обозначението: ще обозначим точките с главни букви с нормален шрифт (например: A, B), а радиус-векторите на точките (и правилните вектори) с получер курсив (например A, G, BC, b).
1. Центроид на триъгълник. Точката G от пресечната точка на медианите на триъгълника ABC се нарича негов център. Изразяваме радиус вектора G на центроида чрез радиус векторите A, B, C на върховете на триъгълника за всеки избор на началото на векторите - точката O.
По свойството на медианите на триъгълник CG:GM=2 (виж фиг.1), следователно G=(C+2M)/3, където M е средата на страната AB, т.е. M=(A+B)/2. Така,
Обратното също е вярно: ако точките A, B и C не са колинеарни и е изпълнено условие (1), то точка G е центроидът на триъгълник ABC. Наистина, нека точката M е средата на отсечката AB, т.е. за произволен избор на началото на векторите O имаме M=(A+B)/2. Тогава от равенство (1) получаваме G=(C+2M)/3, т.е. G разделя медианата CM в съотношение 2:1 и следователно е центроидът на триъгълника ABC.
2. Ортоцентър на триъгълник. Правата линия на Ойлер. Ако вземем центъра O на окръжността, описана около триъгълника ABC, като начало на векторите, тогава радиус векторът на ортоцентъра H (точката на пресичане на височините) на този триъгълник е равен на
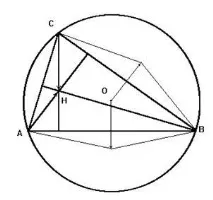
Фигура 2. Ортоцентър на триъгълник
Наистина, векторите A+B и H-C (виж Фиг. 2)са колинеарни, така че A+B = l(H-C).
По същата причина B+C = m(H-A).
След изваждане член по член на тези равенства, получаваме:
A-C = (l - m)H - lC + mA или
(1 - m)A + (l - 1)C + (m - l)H = 0
и сумата от коефициентите
(1 - m) + (l - 1) + (m - l) = 0.
Изпълнението на тези две условия е възможно само в два случая:
или когато точките A, C и H са колинеарни (това е невъзможно поради условието), или когато
(1 - m) = (l - 1) = (m - l) = 0.
Така че последното е:
Тъй като за всеки избор на произход на векторите на точка O
тогава в този случай G = H/3, т.е. точките O, G и H са колинеарни и OG : GH = 1:2. Правата OGH се нарича линия на Ойлер за триъгълника ABC.
Теорема 1: Точките, симетрични на ортоцентъра на триъгълник по отношение на неговите страни и среди на страните, лежат върху окръжност, описана около този триъгълник.
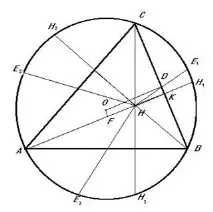
Доказателство: Да вземем центъра на описаната окръжност за начало на радиуса - вектори на точки. Ако точката E1 е симетрична на H по отношение на средата на страната BC (виж фиг. 3), тогава:
E1 = B + C - H = -A, т.е. точки A и E1 са диаметрално противоположни и
Нека правата AN пресича правата BC в точка K, а окръжността - в точка H1. Ако OD е перпендикулярна на BC и OF е перпендикулярна на AK, тогава:
K = D + F, D = (B + C) / 2, F = (A + H1) / 2 и следователно K = (B + C + A + H1) / 2 = (H + H1) / 2, т.е. H1 е симетрична на точката H спрямо правата BC. За точките H2 и H3 доказателството е подобно.
Теорема 2: Във всеки триъгълник средите на страните, основите на височините и трите точки, които разполовяват сегментите на височините от върховете до ортоцентъра, лежат на една окръжност, наречена окръжност с девет точки на триъгълника.
Доказателство: За начало на векторите вземаме центъра O на окръжността, описана около триъгълника(виж фиг. 4). Означаваме с Oi средите на страните, с Hi основите на височините, с Ki средите на сегментите на височините от ортоцентъра до върха (i = 1, 2, 3).
Ако L е средата на отсечката OH, тогава
L = H/2 = (A + B + C)/2,
LO1 = O1 - L = (B + C)/2 -(A+B+C)/2 = -A/2,
LK1 = K1 - L = (A + H)/2 - H/2 = A/2.
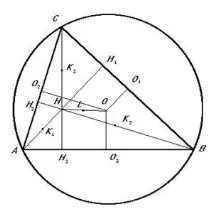
Така точките Оi и Кi (i =1, 2,3) са симетрични спрямо L, т.е. принадлежат на окръжност с център L и радиус, равен на половината от радиуса R на описаната окръжност, тъй като LO12 = LK12 = (±A/2)2 = R2/4. Ъглите ОiHiKi ( i=1, 2, 3) са прави линии и се основават на диаметрите на получената окръжност и следователно принадлежат точките Hi на тази окръжност. По-нататък се спираме на приложението на разгледаните факти към изродени триъгълници, т.е. триъгълници, които имат два или три върха.
3. Триъгълник с два съвпадащи върха.
Ако върховете B и C на триъгълника ABC съвпадат, тогава страната BC \u003d a ще бъде допирателна към окръжността, описана около триъгълника в тази точка, а дължината на страната BC ще бъде равна на нула.
И така, можете да дефинирате триъгълник с два съвпадащи върха (изроден триъгълник) по два начина:
1) това е хорда AB на окръжност с един двоен край B;
2) е отсечка AB и права, минаваща през нейната точка B.
В последния случай окръжността, описана около триъгълника ABC, се допира до правата a в лежащата върху нея точка B. Този кръг е уникален.
В получения триъгълник с два съвпадащи върха ъгълът A е равен на нула, а ъглите B и C са съседни, така че сумата от вътрешните ъгли на триъгълника е 1800. Помислете за интерпретацията на свойствата на неизроден триъгълник за този триъгълник.
И така, за всеки избор на началото O на векторите G=1/3(A+2B), т.е. центроид G делиотсечка AB спрямо l=2:1. Ортоцентърът H се определя и като пресечната точка на височината AHi ^ a и двойната височина, минаваща през точката B є C, перпендикулярна на AB. Ако вземем центъра O на описаната окръжност като начало на векторите, тогава H \u003d A + 2B (фиг. 5).
Така че векторите G и H са колинеарни и OG : GH = 1 : 2.
Приложена към този случай, теорема 1 гласи следното:
Ако AB е хордата на окръжността, a е допирателната към нея в точка B и перпендикулярите от точка A към правата a от точка B на правата AB се пресичат в точка H, тогава точките E, F и K, симетрични на H съответно спрямо a, B и средата на AB, принадлежат на тази окръжност (фиг. 5).
За обикновен триъгълник теоремата на Симпсън важи:
ортогоналните проекции на точка от окръжност върху страните на вписан в нея триъгълник лежат на една права линия, наречена линия на Симпсън за дадения триъгълник.
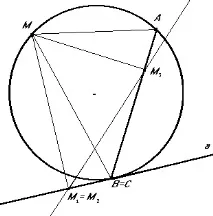
За изроден триъгълник този факт е тривиален: точките M1 и M2 съвпадат, а две точки M1 є M2 и M3 винаги определят права линия (фиг. 6).
Въпреки това, тъй като DMM1B
DMM3A, (те са правоъгълни и ъглите MVM1 и MAM3 се измерват с половината дъга MnB), тогава MB: MA = MM2: MM3 или MB MM3 = MA MM2, т.е. получаваме теорема 3:
Ако AB е хорда на окръжност и a е допирателна към нея в точка B, тогава произведението на разстоянията на произволна точка от окръжността до допирателната точка и до хордата е равно на произведението на разстоянията на тази точка до втория край на хордата и до допирателната.
Теорема 2 (за кръга от девет точки на триъгълник) за изроден триъгълник може да се формулира по следния начин:
Ако AB е хорда на окръжност, a е допирателна към нея в точка B и перпендикулярите AH1 към правата a и FB към правата AB се пресичат в точка H (фиг. 5), то основите H1 и B на тези перпендикуляри и средите на отсечките AB,AH и BH лежат на една и съща окръжност, чийто радиус е равен на половината от радиуса на дадената окръжност.
Триъгълник с три съвпадащи върха (двойно изроден триъгълник).
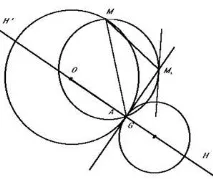
Такъв триъгълник може да бъде определен с помощта на точка А от окръжността (фиг. 7). В този случай и трите страни съвпадат, тъй като A=B=C, и се допират a до окръжността в точка A. Ако приемем центъра O на описаната окръжност за начало на векторите, то G=A и H=3A, т.е. OAN - права линия на Ойлер за изроден триъгълник и OG:GH=1:2. Точката H', симетрична на H спрямо страните и средите на страните на изродения триъгълник ABC, лежи върху окръжността (O, OA), описана около този триъгълник.
За да разберете позицията на Симпсъновата линия, нека се обърнем към фиг.6. Тъй като PMM1B = PMM3B = 900, тогава точките M1 е M2 и M3 принадлежат на окръжността с диаметър MB. Следователно, ако A=B, тогава правата на Симпсън M1M3 ще се допира в точка M1 до окръжност с диаметър MA=MB (фиг. 7).
Окръжността на деветте точки на триъгълника ABC е окръжността, допирателна към описаната окръжност в точка A (основата на трите височини, средата на трите страни) и минаваща през средата на отсечката HA, т.е. неговият радиус е равен на половината от радиуса на дадения кръг.
Майоров В.М., Скопец З.А. Векторно решение на геометрични задачи. М. - Просвещение, 1968.
Скопец З.А., Панарин Я.П. Геометрия на тетраедъра и неговите елементи. Ярославъл, 1974 г.