Основата на концепцията за стереометрия
I. Обобщаване и систематизиране на знанията на учениците
Пространствени геометрични форми
В 7-9 клас се запознахте с планиметрията. Планиметрията е дял от геометрията, в който се изучават свойствата на плоските геометрични фигури: триъгълници, успоредници, кръгове и др.
Но освен плоски фигури има и пространствени фигури: правоъгълен паралелепипед, куб, пирамида, цилиндър, конус, топка. Много предмети около нас имат формата на правоъгълен паралелепипед: класна стая, тухла, кибритена кутийка и др. Популярната в цял свят играчка - кубчето на Рубик - има формата на куб. Добре познатите пирамиди на древен Египет ни дават представа за широк клас геометрични тела, които се наричат пирамиди.
В курса по рисуване и математика от 5-6 клас се научихте да изграждате изображения на тези пространствени фигури. На фиг. 1 е показан правоъгълен паралелепипед.
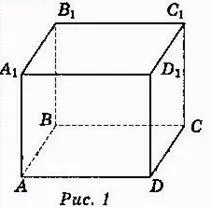
Правоъгълният паралелепипед е пространствена геометрична фигура, ограничена от шест правоъгълника, наречени лица. Страните на правоъгълниците се наричат ръбове на кубоида.
Наименувайте върховете, ръбовете, лицата на правоъгълния паралелепипед, показан на фиг. 1.
Кубът е правоъгълен паралелепипед с всичките шест лица на квадрат (фиг. 2).
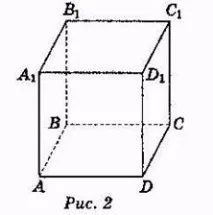
Назовете предната, задната, лявата, дясната, горната и долната страна на куба, показан на фигура 2.
Горната и долната страна на правоъгълен паралелепипед се наричат основи, а ръбовете на тези лица се наричат основни ръбове, другите ръбове се наричат странични ръбове, а останалите лица се наричат странични лица.
Наименувайте страничните ръбове на кубоида (вижте фиг. 1) и куба (вижте фиг. 2).
n-ъгълна пирамида се наричагеометрично тяло, ограничено от n-ъгълник (който се нарича основа на пирамидата) и n триъгълника (странични лица) с общ връх (който се нарича връх на пирамидата). На фиг. C изобразява триъгълна пирамида, която също се нарича тетраедър, на фиг. 4 - четириъгълна пирамида.
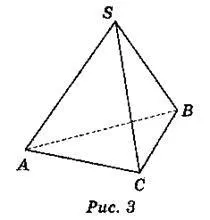
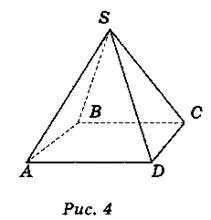
Назовете основите, страничните лица, страничните ръбове, базовите ръбове, върховете на пирамидите, показани на фиг. 3 и 4.
Паралелепипедите и пирамидите са представители на голям клас геометрични фигури, наречени полиедри. В допълнение към полиедрите геометрията разглежда и други пространствени фигури: цилиндри, конуси, топки и др.
Разделът от геометрията, в който се изучават свойствата на пространствените фигури, се нарича стереометрия.
В 10 и 11 клас ще изучаваме свойствата на пространствените фигури.
II. Възприемане и осъзнаване на нов материал
Основни понятия на стереометрията
Основните фигури в пространството са точка, права и равнина.
Имате представа за точки и прави от курса по планиметрия. Спомнете си, че точките се обозначават с главни латински букви, например точки A, B, C.; линиите се обозначават с малки латински букви, например линии a, b, c. или две главни букви, например AB, BC, CD .. . Материални модели на част от равнината, например повърхност на маса, повърхност на прозорец, повърхност на мраморна плоча и др. В геометрията се смята, че равнината е неограничена, идеално плоска и гладка.
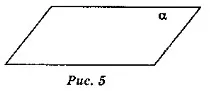
Те се изобразяват на равнина под формата на успоредник (фиг. 5) или под формата на произволна област (фиг. 6).
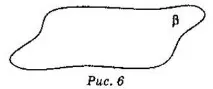
Обозначете равнините с гръцки букви, например α, β, γ. На фиг. 5 показва равнината α на фиг. 6 - равнина β. Фасетиполиедри са части от равнини.
Както всяка геометрична фигура, равнината се състои от точки. Ако точката A лежи в равнината α, казват, че равнината α минава през точката A, и записват: A α. Ако точката A не лежи в равнината α, казват, че равнината α не минава през точката A, и пишат: Aα.
Ако всяка точка от правата a лежи в равнината α, казват, че правата a лежи в равнината α или равнината α минава през правата a и пишат: a α. Означението α означава, че правата a не лежи в равнината α.
Съставете и напишете със символи:
а) равнината α и лежащата в нея точка A;
б) равнината α и нележащата в нея точка B;
в) равнината β, която минава през правата a;
г) равнината γ и правата a, която не лежи в равнината γ;
д) две равнини α и β, които минават през правата c.
Както и в планиметрията, свойствата на основните фигури в стереометрията се изразяват с аксиоми.
Спомнете си, че в планиметрията свойството на линиите и точките беше изразено чрез аксиомата:
Каквато и да е правата, има точки, които й принадлежат, и точки, които не й принадлежат.
Например на фиг. 3 точки A и B принадлежат на правата AB, но точките S и C не й принадлежат.
Дадена е равнина (например равнината на пода на класна стая), можем да посочим точките, които принадлежат на тази равнина, и точките, които не й принадлежат. Следователно едно от свойствата на равнината е аксиома C1:
Каквато и да е равнината, има точки, които принадлежат на тази равнина, и точки, които не принадлежат.
Използвайки изображението на куба на фиг. 2, посочете точките, които:
а) не включват предната страна;
б) принадлежат към горното лице;
в) принадлежат на лица ABCD ;
г) не принадлежат на лицето A1B1BA.
Помислете за втората аксиома на C2 стереометрията:
Ако две различни равнини имат обща точка, тогава те се пресичат по права линия, минаваща през тази точка.
Ясна илюстрация на тази аксиома е пресечната точка на две стени, стената и пода на класната стая.
С помощта на фиг. 1, моля посочете:
а) общи точки на горната и предната повърхност;
б) линията на пресичане на равнините на задната и долната повърхност;
в) общи точки на равнините на лицата АВВ1А1, и Α1Β1С1 D 1 ;
г) линията на пресичане на равнините на лицата Α1Β1С1 D 1 и ВВ1С1С.
Няма инструменти, които могат да бъдат изнесени в пространството на равнина. Следователно изразът "възможно е да се начертае равнина" се използва в смисъла на "съществува равнина".
Третата аксиома на стереометрията C3 гласи:
Ако две различни прави имат обща точка, тогава през тях може да се начертае само една равнина.
1. С помощта на фиг. 1, посочете коя равнина определят линиите:
2. С помощта на изображението на куба на фиг. 2, докажете, че е възможно да се начертае равнина през прави:
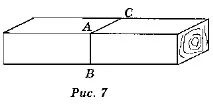
3. За да бъде плоска режещата повърхност на четириъгълната греда (фиг. 7), дърводелецът направи това; отбеляза точка А на ръба на гредата и начерта два сегмента AB и AC от нея в правилната посока в съседните страни на гредата, след което насочи триона по предвидените сегменти. Обяснете, че трябва да се образува равна повърхност на рязане.
4. Дърводелецът с помощта на две нишки проверява дали краищата на четирите крака на стола лежат в една равнина. Как го прави?
Трябва да се отбележи, че в пространството има много равнини и за всяка равнина са валидни всички аксиоми и теореми на планиметрията. Освен това признаците за равенство и подобие на триъгълниците са валидни и за триъгълници, които лежат в различни равнини.
III. Затвърдяване и осмисляне на знанията на учениците
1. Докажете, че върховете на успоредника ABC D лежат в една равнина.
2. Дадени са две прави a и b, през които не може да се прекара равнина. Докажете, че тези прави не се пресичат.
3. Докажете, че две прави в пространството могат да се пресичат в повече от една точка.
4. Могат ли две равнини да имат само една обща точка?
5. Може ли три равнини да имат само една обща точка?
6. През точка са прекарани три прави, които не лежат в една равнина. Колко различни равнини могат да се начертаят през тези прави, като се вземат по двойки?
7. Задача No 2 от учебника (стр. 9).
8. Задача номер 5 от учебника (стр. 9).
IV. Домашна работа
§1, т.1; контролни въпроси No 1,2; задачи номер 1, 3 от учебника
V. Обобщаване на урока
Когато обобщавате урока, можете да използвате тази схема.