Основни закони на масообмена
В процесите на прехвърляне на разпределен компонент от една фаза в друга се разграничават два случая: 1) прехвърляне от течен (газов) поток към течен поток или обратно; 2) прехвърляне от твърд към течен (газ) поток или в обратна посока, т.е. пренос на маса между порестата твърда фаза и потока на течната (газообразна) фаза.
Елементарните закони, които управляват прехвърлянето на разпределено вещество от една фаза в друга, сазаконите на молекулярната дифузия, масовия трансфер и масовата проводимост.
Законът за молекулярната дифузия (първият закон на Фик).Молекулярната дифузия в газове и разтвори на течности възниква в резултат на хаотичното движение на молекулите, което не е свързано с движението на флуидните потоци. В този случай молекулите на разпределения компонент се прехвърлят от региони с високи концентрации в региони с ниски концентрации. В този случай кинетиката на преноса се подчинява на първия закон на Фик, чиято формулировка е подобна на закона за топлопроводимостта:количеството вещество, дифузирало във фазата, е пропорционално на градиента на концентрация, площта, перпендикулярна на посоката на дифузионния поток, и времето
,
където е коефициентът на пропорционалност иликоефициентът на дифузия.
.
Коефициентът на дифузия показва какво количество вещество дифундира през повърхността от 1 m2 за 1 s с разлика в концентрацията на разстояние 1 m, равна на единица.
Знакът минус от дясната страна на уравнението показва, че по време на молекулярна дифузия посоката на движение на веществото и концентрационният градиент са противоположни един на друг.
Размерността на коефициента зависи от начина на изразяване на концентрацията на разпределения компонент. Ако това са обемни концентрации, тогава размерът на коефициента е както следва:
==.
Коефициентът на дифузия не е постоянна стойност. Това е сравнително малка стойност за газове. То е с четири порядъка по-високо, отколкото при течности. Коефициентът на дифузия се увеличава с повишаване на температурата и намалява с увеличаване на налягането. Ако в газовете коефициентът на дифузия не зависи от концентрацията на дифузиращото вещество, то в течностите този ефект е особено важен за неразредени разтвори.
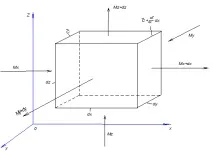
Ориз. 4.8. Относно извеждането на диференциалното уравнение на молекулярната дифузия
Ако едно разпределено вещество се движи през този елементарен паралелепипед поради молекулярна дифузия, то през лявата, задната и долната стени за определен период от време в него постъпват количествата на веществото, съответно и , а през противоположните стени - дясната, предната и горната, постъпват количествата на веществото съответно и . Следователно елементът за определен период от време придобива дифузно вещество в количество
.
В този случай концентрацията на дифузиращото вещество се увеличава с .
Според основното уравнение на молекулярната дифузия, ,
.
.
; .
Обобщавайки лявата и дясната част на последните три равенства, получаваме:
.
От друга страна, същото увеличение на количеството дифундиращо вещество в елемента може да се намери чрез умножаване на обема на елемента по промяната в концентрацията във времето, т.е.
.
Приравнявайки десните части на последните две зависимости, получаваме уравнението на молекулярната дифузия:
. (4.17)
Лявата страна на това уравнение характеризира локалната промяна в концентрацията на компонента, който трябва да се разпредели в неподвижния елемент, изолиран във фазата на разпределение.
Закон за пренос на маса (Щукарев). Основният закон на масовия пренос или конвективната дифузия е формулиран за първи път от Шчукарев при изучаване на кинетиката на разтваряне на твърди вещества. Този закон е аналогичен на закона за пренос на топлина, формулиран от Нютон.
Количеството вещество, прехвърлено от интерфейса към приемащата фаза, е пропорционално на разликата в концентрациите в интерфейса и в ядрото на потока на приемащата фаза, контактната повърхност на фазата и времето:
, (4.18)
където е коефициентът на масов пренос, характеризиращ преноса на вещество във фазата чрез конвекция и дифузия едновременно; е концентрацията на разпределения компонент на границата на разпределителната фаза; е концентрацията на разпределения компонент в ядрото на потока на разпределителната фаза.
Имайте предвид, че концентрацията на границата се счита за равновесна концентрация.
Размерът на коефициента на масов трансфер може да се определи от уравнението
=.
Коефициентът на масов трансфер показва колко вещество се прехвърля от фазовия интерфейс към приемащата фаза презповърхност от1 m2 за 1 s при разлика в концентрацията, равна на единица.
За постоянен процес коефициентът на масов трансфер и концентрация остават постоянни в разглеждания обем:
. (4.19)
Ако коефициентът на масов трансфер остане постоянен за цялата повърхност, тогава уравнението става:
. (4,20)
Диференциално уравнение на масовия пренос (конвективна дифузия). Разглеждането на явлението конвективна дифузия се основава натеория на дифузионния граничен слой.
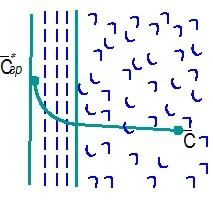
Ориз. 4.9. Относно формулирането на закона за конвективната дифузия
Разглежданата система се състои от две части: ядро и граничен дифузионен слой, който включва доста тънък ламинарен подслой. В ядрото преносът на материя се извършва главно от флуидни течения при условия на достатъчна турбулентност. Концентрацията на разпределения компонент в ядрото на турбулентния поток на фазата се приема за постоянна ().
С приближаването на граничния дифузионен слой турбулентният транспорт се разпада и с наближаването на фазовата граница транспортът, дължащ се на молекулярна дифузия, започва да преобладава в ламинарния подслой. Съответно се появява градиент на концентрация на разпределения компонент, който се увеличава с приближаването му до границата. По този начин областта на дифузионния граничен слой е областта на проявление и нарастване на молекулярната дифузия от малка до максимална стойност.
При наличие на конвективна дифузия концентрацията на разпределения компонент се променя не само поради молекулярна дифузия, но и поради механичното му пренасяне от една област на пространството в друга. В този случай концентрацията на разпределения компонент ще бъде функция не само на координатитеx,y,zи времето, но също така и компонентите на скоростта на движение на частиците на потока.
При конвективната дифузия безкрайно малък елемент на потока се движи от една точка в пространството в друга. В този случай промяната в концентрацията на разпределения компонент може да бъде изразена чрез субстантивната производна, която отчита промяната в неговатавъв времето и промените, свързани с движението на елемент от една точка в пространството в друга:
. (4.21)
В това уравнение е локална промяна в концентрацията на разпределения компонент, а комплексът е конвективна промяна в концентрацията.
Ако в уравнението на молекулярната дифузия (4.17) заместим локалната промяна в концентрацията с обща промяна, в съответствие с уравнение (4.21), тогава можем да получим диференциално уравнение за конвективна дифузия:
. (4.22)
Уравнението на конвективната дифузия трябва да се решава заедно с уравненията на движението на Навие-Стокс, тъй като променливите са концентрации и проекции на скоростта на потока. Тази система от уравнения обаче няма аналитично решение и за да се получат изчислените зависимости за масов пренос, трябва да се прибегне до теорията на подобието.