Приемане на кодови комбинации в дискретни комуникационни канали с шум

Теория на информацията

Информационна поддръжка на системи за управление

Трансфер на данни

По-горе бяха разгледани методи за получаване на елементарни сигнали, които предават отделни символи на кодовата комбинация. Но съобщенията в реалните системи се предават не като отделни знаци, а като комбинации от знаци (кодови комбинации).

Ако има смущения в комуникационния канал, тогава един или повече символи от кодовата комбинация ще бъдат изкривени. В резултат на това има три основни случая на декодиране (декодиране) на получената кодова комбинация:

правилно приемане на съобщение с вероятностP PR(обикновеноP PRi 0.999);
фалшиво приемане на съобщение с вероятностP L PR(P L PRЈ 10 -7 ), т.е. фалшивото приемане трябва да бъде практически изключено);
защитно отхвърляне, когато се получи кодова дума, която не може да бъде идентифицирана с нито едно съобщение в списъка, т.е. без разрешена кодова дума.

В случай на правилно или фалшиво приемане, системата получава съобщението, без да знае дали е било изкривено в комуникационния канал. Сумата от вероятноститеP PRиP L PRе вероятността за приемане като цяло. Вероятността за защитна повреда може да се изчисли по формулата

Не можете да изчислите всички тези вероятности, но се съсредоточете върху две от тях. Една от избраните вероятности задължително трябва да бъде вероятността за фалшиво приемане.

Можем да говорим за друга възможност: вероятността да фалшифицирате съобщение. Това е случай на фиксиране на съобщение от приемащата страна в случай, че изобщо не е предадено нищо. Такава ситуация се случва изключително рядко, така че тази вероятност се оценява от броя на съобщенията за няколко години и доридесетилетия.

Качеството на системата се оценява не по вероятността за правилно, а по вероятността за погрешно приемане.

Вероятностите за правилно, фалшиво приемане и защитна повреда зависят както от характеристиките на комуникационния канал (q, p 0, p C), така и от броя на грешките в кодовата дума.

Броят на грешките обикновено се характеризира с кратносттаt. В този случай кодовата комбинация може да бъде изкривена от различен брой грешки във всички възможни комбинации от 0 доt.

В предавателните системи се говори за вектор на грешка. Това е число вK-арната система с обща стойностn(тя е равна на стойността на предадената кодова комбинация) и нула символи на неизкривени позиции. Например, в бинарни комуникационни канали, при предаване на шестбитова кодова дума, могат да работят следните вектори на грешки:

В първия случай персонажът на трета позиция е изкривен, във втория случай героите на първа и трета позиция са изкривени.

За двоичната версия векторътEсе определя от теглото на грешкатаV(E). По-нататък ще приемем, че се използва двоичен комуникационен канал.

Изкривяването на предадената комбинация може да бъде математически представено чрез сумиране по модул две на неизкривената кодова думаAи вектора на грешкатаE:

Да приемем, че съобщенията се предават в някои комбинации с дължинаnпо симетричен комуникационен канал с параметриqиp 0. Нека предадената комбинация бъде засегната от вектора на грешкатаEiс теглоi. Вероятността кодовата комбинация да съдържаiгрешки може да се изчисли по формулата

Грешка в множественосттаiможе да възникне в

случаи, но общата вероятност за поява на грешки с множественостtв кодова дума отnгерои

Нека определим вероятностите за правилно приемане, фалшиво приемане и защитна повреда при използване на различни кодове.

Неизлишен код. За такъв кодt= 0, тоест той не може не само да коригира, но дори да открие една грешка.P PR= (1 –p0)n, тоест нито един отnелементите не е изкривен, тъй като кодът не е излишен. (членът приi= 0 е вероятността за правилно приемане).P З OT= 0. Нека оценим вероятността за фалшиво приемане, приемайкиp 0» 10 -4; P L PR»n10 -4 . По този начин нередундиран код не може да се използва в комуникационни канали със смущения, тъй като се характеризира с висока вероятност за фалшиво приемане.
Излишен код в режим на откриване на множествена грешкаr.P PR= (1 –p0)n, Защитната повреда може да възникне не само при грешки с кратност по-малка отr, но и в други случаи (AiЈC i n). Вероятност за фалшиво приеманеBiJC i n;Bi = C i n – Ai. СтойноститеAiиBiсе изчисляват експериментално. С оглед на ниската вероятностр 0, когато се изчислява вероятността от защитна повреда, можете да се ограничите до няколко термина: и при определяне на вероятността от фалшиво приемане, само първия член.
Излишен код в режим на откриване наkгрешки и коригиране наsот тях.

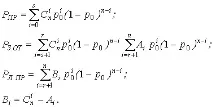
В шумен комуникационен канал единственият рационален начин за предаване на информация е да се използват излишни кодове, способни да откриват и/или коригират грешки.

Нека сега разгледаме по-подробно начините за конструиране на такива кодове. Те са разработени според различни теории за кодиране. Двата най-развитиклонове на теоретичното изграждане на кодове: комбинаторни и алгебрични. Теорията на комбинаторното кодиране се основава на комбинаториката - дял от математиката, който изучава свойствата на разположенията, пермутациите, комбинациите. Започва да се развива в средата на 19 век. Теорията за алгебричното кодиране възниква в края на 50-те и началото на 60-те години на миналия век.