Проблем с Рамзи
Следният пъзел е широко известен.
Докажете, че сред всеки шестима души има или трима по двойки познати, или трима по двойки непознати. Тази ситуация може да бъде описана с граф G с шест върха, представляващи хора; съседството на два върха съответства на запознаване. Изисква се да се покаже, че G съдържа или три по двойки съседни, или три по двойки несъседни върха.
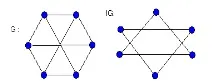
ДопълнениетоG на графа G има множеството V(G) като множество от върхове, два върха в G са съседни тогава и само ако не са съседни в G. графиката G няма триъгълници, а графиката G има точно два.Самодопълваща се графикае графика, изоморфна на своя комплемент. Примери за такива графики са показани на фигурата.
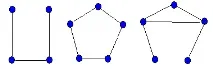
В пълния граф Kpвсяка двойка от неговите p върхове е съседна. Така графиката Kp има (P2) ребра и е правилна от степен p-1. Графиката K3 е триъгълник. Графики !Kp—напълно несвързани(или редовни степени 0).
В тези условия пъзелът може да се формулира по следния начин:
Теорема.Ако G е графика с шест върха, тогава G или !G съдържа триъгълник.
Доказателство. Нека v е произволен връх на граф G, който има шест върха. Тъй като върхът v е съседен на всеки от останалите пет върха в G или в G, тогава, без загуба на общност, можем да приемем, че върховете u1,u2,u3 са съседни на v в G. Ако всеки два от върховете u1,u2,u3,са съседнив G, тогава заедно с v те образуват триъгълник. Ако нито един от тях не е съседен в G, тогава върховете u1,u2,u3 в графа G образуват триъгълник.
Обобщавайки теоремата, естествено е да зададем въпроса: кое е най-малкото цяло число r(m,n), за което всяка графика с r(m,n) върхове съдържа Km или Kn
Числата r (m,n) се наричатчисла на Рамзи. Ясно е, че r(m,n) =r(n, m). Проблемът, свързан с намирането на числата на Рамзи, остава нерешен, въпреки че е известна проста горна граница, получена от Erdős и Székeres:
Изложението на този проблем следва от теоремата на Рамзи. Един безкраен граф има безкраен брой върхове и не съдържа множество ребра или цикли. Рамзи доказва (на езика на теорията на множествата), че всеки безкраен граф съдържа #0 по двойки съседни върхове или #0 по двойки несъседни върхове.
Всички известни числа на Рамзи са дадени в табл.
3 3 6 9 14 18 23
Екстремални графики
Сред първите резултати в една от областите на теорията на графите - теорията на екстремалните графи - можем да отбележим следната добре известна теорема на Туран [1]. Както обикновено, нека [r] е най-голямото цяло число, не по-голямо от реалното число r, и нека = е най-малкото цяло число, не по-малко от r .
Теорема:Най-големият брой ребра в графики с p върха и без триъгълници е[p2/4].
Доказателство: Твърдението е очевидно за малки p стойности. Доказателството чрез индукция може да се даде отделно за нечетно и четно p; тук ще бъде разгледан само случай на четни p стойности. Да приемем, че твърдението е вярно за всички четни стойности на p 2 /4] ръбове.
За да завършим доказателството, остава да установим, че за всяко четно p съществува (p, P 2 /4)-граф, който не съдържа триъгълници. Такава графа може да бъде формирана по следния начин: вземете две групи V1 и V2, всеки от които има p/2 върха, и свържете всеки връх от V1 към всеки връх от V2.
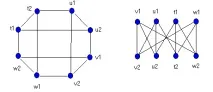
Двустранен граф(илибиграф) G е граф, чието множество от върхове V може да бъде разделено на две подмножества V1 и V2 по такъв начин, че всяко ребро на графа G свързва върхове от различни множества (ще кажем, че ръбоветеграфика G свързва множествата V1 и V2) - Например графиката, показана на фиг. отляво можете да нарисувате, както е показано на фигурата вдясно, за да подчертаете, че тази графика е двустранна.
Ако граф G съдържа всички ребра, свързващи множествата V1 и V2, тогава този граф се наричапълен двустранен. Ако множеството V1 има m върха и V2 има n върха, тогава пишем G =Km,n.= K(m,n).Звездатае пълен двустранен граф K1,n. Ясно е, че графиката Km,n има mn ребра. Следователно, ако p е четно, тогава графиката K(p/2, p/2) съдържа p2/4 ребра; ако p е нечетно, тогава графиката K([p/2], ) съдържа [p/2] = [p2/4] ребра. Във всяка от тези графики няма триъгълници, което следва от теоремата на Кьониг
Теорема:Графиката е двустранна тогава и само ако всички нейни прости цикли са четни.
Доказателство. Ако G е двустранен граф, тогава множеството от неговите върхове V може да бъде разделено на две подмножества V1 и V2 по такъв начин, че всяко ребро на този граф свързва някакъв връх от множеството V1 с някакъв връх от V2. Следователно всеки прост цикъл v1v2. vnv1 на G съдържа върхове от V1 с, да речем, нечетни числа и върхове от V2 с четни числа, така че дължината n на този цикъл е четно число.
За да докажем обратното, предположим без загуба на общност, че G е свързана графа (тъй като всеки компонент на G може да се разглежда отделно). Вземете произволен връх vjV и означете с V1 множеството, състоящо се от v1 и всички върхове, разположени в графа G на равно разстояние от v1; нека V2=V-V1. Тъй като всички прости цикли на графа G са четни, всяко негово ребро свързва множествата V1 и V2. Наистина, ако има ребро uv, свързващо два върха от множеството V2, тогава обединението на геодезичните, преминаващи от върха v1 към върха u, а също и отвръх v1 до връх u, заедно с ръба uv образува цикъл с нечетна дължина; стигнахме до противоречие.
Теоремата е първият пример за решаване на един от проблемите на "теорията на екстремалните графи": за даден граф H, намерете ex(p, H) - най-големият брой ребра, които могат да бъдат в граф, който има p върха и не съдържа забранен подграф H. Така теоремата гласи, че ex (p, K3) = [p*p/4]. Ето някои други подобни резултати (Erdős [3]):
Известно е също, че всеки (2n, n*n+1)-граф съдържа n триъгълника, всеки (p, 3p-5)-граф съдържа два прости цикъла без общи ребра (за p>= 6) и всеки (3n, 3n2 + 1)-граф съдържа n2 прости цикъла с дължина 4.