Рандомизиран алгоритъм

Министерство на образованието на Руската федерация

Държавен университет в Санкт Петербург

Рандомизиран алгоритъм за конструиране на изпъкнала обвивка

Формулиране на проблема:

Разработете и напишете програма за рандомизиран алгоритъм за конструиране на изпъкнала обвивка, базирана на изходните данни от дипломната работа. Подобрете визуализацията на алгоритъма. Добавете изчисляване на времето за изпълнение на алгоритъма.

Означаваме изпъкналата обвивка на множеството от точкиSсconv(S). Границатаconv(S)образува изпъкнал многоъгълник, чиито върхове са подмножество отS. Винаги, когато няма опасност от объркване, ще наричаме този многоъгълник катоconv(S).Проблемът с изчисляването на изпъкналата обвивка в равнината е следният: при даденSсе изисква да се изчисли многоъгълникът (ограничаващ)conv(S).Резултатът трябва да бъде представен като списък, съдържащ точкитеS, които са върховете наconv(S), изброени обратно на часовниковата стрелка според външния им вид в многоъгълник; началната точка за списъка може да бъде произволна. За категоричност ще приемем, че първата точка в това подреждане е точката отS, която има най-малкатаx- координата. За простота приемаме, че вSняма три точки, лежащи на една права. Когато бъде приложено, това предположение може да бъде изоставено.

Нека покажем как рандомизираната стъпка по стъпка конструкция, описана по-горе (в раздел 3.1.) в контекста на сортирането, може да се приложи към този проблем.

Алгоритъмът първо произволно пренарежда точките във входния наборS. Некаpiеiта точка в това произволно подреждане (1 ≤i≤n).НекаSiе колекцията p1, …,pi>. След това алгоритъмът продължава наnстъпки. Следiта стъпка, алгоритъмът ще изчислиconv(Si). Наiта стъпкаpiсе добавя къмconv(Si-1), образувайкиconv(Si). Сега нека дефинираме подробностите за тази стъпка на модификация.

нека винаги съхраняваме точката във вътрешната областconv(S); по-специално, можем да използваме центъра на масатаconv(S3)за тази цел (който може да бъде изчислен в постоянно време). Нека означим тази точка сp0. Освен това, следiта стъпка, имаме списък, съдържащ върховетеconv(Si). В допълнение, за улеснение на описанието, ние приемаме, че този списък също така съдържа ръбове, свързващи следващите върхове в този списък (това може лесно да бъде избегнато при изпълнението с малко допълнителна работа). НекаS\Si-е наборът от точки, които да бъдат добавени следiта стъпка, 3 ≤i≤ (n-1). За всяка точкаpS\Siсъхраняваме (двупосочен) указател отpкъм странатаconv(Si), пресечена от лъч, който произхожда отp0и минава презp. Ще кажем, чеpпресичададеното реброconv(Si). По този начин, при даден ръбconv(Si), можем да изброим всички точкиp, които пресичат този ръб във времето линейно в зависимост от броя на тези точки.

След като дефинирахме структурите от данни, ще опишем действията, които са необходими за актуализиране на тези структури на всяка стъпка. Точкатаpi, вмъкната наiта стъпка, е вътре или извънconv(Si-1). Използване на сегментpip0и свързания указател, винаги можем да определим позицията наpi(нашето предположение, че нито една три точки не са колинеарни, изключва възможносттаpiда бъде на границатаconv(Si-1)). Акоpiе вътре вconv(Si-1), премахваме указателя отpiи отиваме на стъпка (i+1). В противен случай, акоpiе извънconv(Si-1), трябва да актуализираме списъка, който е многоъгълник, ограничаващ обвивката. Върховетеconv(Si-1)са разделени на три групи чрез добавяне наpi:

1. Върховеconv(Si-1), които трябва да бъдат премахнати, защото не са върховеconv(Si).

3. Върховеconv(Si-1), които остават вconv(Si)със съответните им ръбове.

Ясно е, че крайните точки на ръба, пресечен от сегментаpip0се отнасят за (1) или (2). Тръгвайки от(в двете посоки) през списъка с върхове, представляващиconv(Si-1), можем да намерим върхове от типове (1) и (2). Ние правим това във времето, линейно зависимо от броя на тези върхове. Докато правим това, намираме точкитеS\Si, които пресичат вече премахнатите ръбове, и актуализираме указателите им към ръбаpiv1или ръбаpiv2. Това отнема постоянно време (защото трябва да проверим само два ръбаpiv1иpiv2) за всяка точка вS\Si, чийто указател трябва да се актуализира (Фигура 5).

Ориз. 5: Изпъкнала обвивкаconv(Si-1). При добавяне наpiкъмconv(Si-1)върховетеsиtсе изтриват и указателят за точкаqтрябва да се актуализира, докато указателят заrне.

Каква е общата работа, извършена наi-та стъпка? Цената за изтриване на ръбаconv(Si-1)е същата като цената на създаването му, тъй като ръбът може да бъде изтрит само веднъж след създаването. Тъй като във всяка стъпка се създават само два ръба, общият брой на тези създаване/изтриване на ръбове (за всички стъпки) е 2nв най-лошия случай.

Що се отнася до разходите за актуализиране на указатели наiта стъпка, това е броят точкиpотS\Si,така чеpp0пресича ръба, който е премахнат на тази стъпка. За да ограничим математическото очакване на тази случайна променлива, прибягваме до обратен анализ. Тоест, представете си, че алгоритъмът се изпълнява обратно и ние ще премахнем точкатаconv(Si\S3),, за да образувамеconv(Si-1). Тогава броят на указателите, актуализирани наiта стъпка на оригиналния алгоритъм, е същият като броя на указателите, премахнати на съответната стъпка на обратния алгоритъм. Нека покажем, че очакваният брой актуализирани указатели еO(n/i) в зависимост от всеки фиксиран наборSi\S3, от който премахваме произволна точка в обратната стъпка. Тъй като тази горна граница е валидна за всеки набор отiточки, зависимостта от конкретния наборSi\S3може да бъде игнорирана.

За точкаpS\Si, некаepе ръбътconv(Si), пресечен отpp0. Вероятността указателятpда е актуализиран е точно вероятносттаepда бъде изтрит в резултат на стъпката на изтриване. Ръб, крайepсе премахва, ако един от двата му върха се премахва в обратната стъпка. Тъй като точката, премахната отSi, е избрана равномерно от (i-3) точки отSi\S3, тази вероятност еO(1/i). Очакваният брой актуализирани указатели еO((n-i)/i), така че общата работа, извършена в тази стъпка, еO(n/i). Ключът тук е, че в стъпката на премахване на обратния алгоритъм, ние премахваме произволна точка отSi, а не случаен връхconv(Si).Сега използваме линейността на очакването, за да ограничим средното време на изпълнение на алгоритъмаO(n log n).

Теорема:Средното време за изпълнение на горния рандомизиран алгоритъм за изчисляване на изпъкналата обвивка на n точки в равнина е O(n log n).

Средното време на изпълнение на този алгоритъм е асимптотично същото като времето на някои известни детерминирани алгоритми с изпъкнала обвивка, по-специално алгоритъма на Греъм, обсъден по-горе, и съответства на неговата долна граница.

В хода на курсовия проект от студентите беше възстановена програма, която реализира изграждането на изпъкнала обвивка с помощта на рандомизиран алгоритъм.

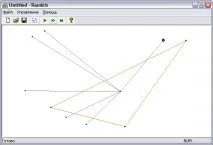
С помощта на менюто Файл можете да записвате, зареждате и изчиствате множество точки.

С помощта на менюто "Контрол" можете да приложите алгоритъма за конструиране на изпъкнала обвивка към набор от точки. С помощта на подточка "По стъпки" можете да следвате всяка стъпка от алгоритъма. Подточката „Връщане към началото“ ви позволява да приведете алгоритъма в първоначалното му състояние.

Подточката "Генериране" ви позволява да генерирате набор от точки според дадените закони за разпределение.

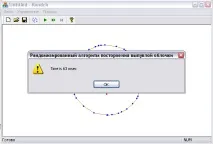
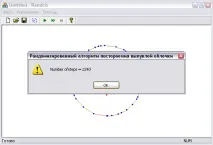
Използвайки подпозицията "Стартиране", можете да кандидатстватеалгоритъм за конструиране на изпъкнала обвивка на набор от точки и вижте броя на стъпките и времето, за което е построен изпъкнал многоъгълник.

Допълнения и промени в програмата:

Оптимизиран е кодът на алгоритъма за намиране на изпъкнала обвивка

Русифицирани елементи от менюто

Подобрена визуализация на алгоритъма (добавен дисплей на текущо обработените върхове и ръбове)

Добавено е изчисляване на времето за работа на алгоритъма.

Разпределение на отговорностите при работа по програмата

Бондарев А. - писане на програмен алгоритъм.

Илина О.К. - писане на интерфейс към програмата.

Добряков М.М. - писане на визуализация на програмата.