Тръбен квартал
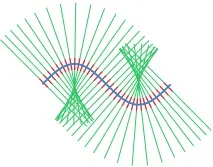
Нека изясним понятието тръбен квартал с прост пример. Да разгледаме гладка крива в равнината без самопресичане. Във всяка точка от кривата начертайте линия, перпендикулярна на тази крива. Ако кривата не е права, тези перпендикуляри могат да се пресичат един друг по доста сложни начини. Въпреки това, ако разгледаме много тясна лента около кривата, частите от перпендикуляри, разположени в лентата, няма да се пресичат и ще покрият цялата крива без празнини. Такава лента е просто тръбна съседство на кривата.
В общия случай, разгледайте подмножеството S\подмножество M на многообразиетоMиNе нормалният пакет към подразнообразиетоSвM. В този случайSиграе ролята на крива, аMиграе ролята на равнина, съдържаща тази крива. Помислете за естественото картографиране
i:N_0 \rightarrow S ,
което установява съответствие едно към едно между нулевия участък N_0 на пакетаNи подмногообразиетоSотM. Некаjе разширение на това преобразуване към целия нормален пакетNсъс стойности в многообразиетоM, къдетоj(N) е отворено множество вM, аjе хомеоморфизъм междуNиj(N). Тогаваjсе нарича тръбен квартал.
Често тръбната околност на подмногообразиетоSсе нарича не самото преобразуванеj, а неговия образT=j(N), като по този начин се предполага съществуването на хомеоморфизъмjмежду множестватаNиT.