Указания Р -2013
5.2 Критерии за количествена оценка
6.1 Примери за изпълнение
6.8 Особено важна зона на защитения обект
Нарязани брезови дърва за огрев с доставка planeta-drov.ru.
5.2. Критерии за количествена оценка
Например проверката на детектор за движение изисква множество нарушения на охраняваната зона, последвани от регистриране на резултатите от експериментите (броя регистрирани нарушения и броя на пропуснатите нарушения).
Въз основа на тези експерименти се изчислява вероятността за правилното функциониране на алгоритъма (в примера по-долу, вероятността за откриване (P obt.)).
Тези оценки могат да се основават на стандартни методи за оценка на „гости“, например на методологията, описана в ST SEV 5313-85 „Приложна статистика. Правила за определяне на доверителните граници за биномни и отрицателни биномни разпределения”.
Тази техника е по-лесна за разбиране и прилагане.
Тази техника се основава на разбирането, че с намаляване на броя на извършените тестове получаваме вероятността за събитие, което е в определен доверителен интервал, т.е. в обхвата на възможните грешки (за по-строга математическа дефиниция на доверителния интервал трябва да се обърнете към E.S. Wentzel „Теория на вероятностите“).
Помислете за примера за изчисляване на вероятността от събитие.
Проведени са 5 експеримента, от които е установена инвазията в 4 случая, Robn=4/5=0,8.
Забележка. Вероятност за събитие
където m е броят на срещанията на A; n е общият брой извършени експерименти.
След това трябва да определим доверителния интервал за тази вероятност.
Забележка. Доверителен интервал - интервалът от стойности на параметрите, които са съвместими с експерименталните данни и не противоречатim.
Обръщаме се към графиката за определяне на доверителния интервал, взет от E.S. Вентцел "Теория на вероятностите" издателство "Наука" 1969, Фиг. 14.5.2 Графиката е показана по-долу.
На тази графика стойностите на доверителния интервал са нанесени вертикално, а вероятността от събитие в нашите експерименти е нанесена хоризонтално. Числото над линиите на графиката показва броя на извършените експерименти (в този случай 5 експеримента).
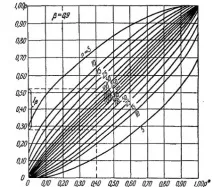
Фиг. 18 - Графика за определяне на доверителния интервал
Тази графика показва, че вероятността за откриване на Robn=0,8 (т.е. извършени са пет експеримента, четири от които се оказват положителни. Robn=4/5=0,8). В този случай стойността на доверителния интервал е от 0,42 до 0,97 с вероятност β = 0,9.
Стойността от броя на експериментите не може да бъде намалена, тъй като границите на доверителния интервал вече са доста големи.
Не е желателно да се намаляват резултатите от положителните експерименти. Намаляването на тези резултати дори с една стойност (т.е. проведени са пет експеримента, три от които са се оказали положителни. Robn = 3/5 = 0,6), дава Robn = 0,6 (въпреки че този резултат може да бъде приемлив при трудни работни условия или с многолинейна защита).
Увеличаването на броя на експериментите намалява ширината на доверителния интервал, което е положителен фактор.
В някои случаи е възможно да се провеждат експерименти в размер на 100 или повече пъти (например определяне на броя на преминаващите автомобили). Тогава доверителният интервал за вероятността за откриване Robn=0,8 ще бъде само в диапазона от 0,74 до 0,82.
Понякога има случаи, когато са получени 10 откривания в 10 експеримента, но това не означава, че вероятността за откриване е = 1, тогава трябва да се използва друга формула.
В този случай вероятността се изчислява въз основа на факта, чесъбитието не е настъпило, т.е. не е намерен (виж по-долу).
където β е достатъчно голяма доверителна вероятност (в нашия пример β =0,9), n е броят на експериментите.
При пет положителни експеримента (n=5) имаме , което означава, че вероятността за неоткриване е 0,369, т.е. вероятност за откриване 1-0,369=0,631.
Закръглявайки нагоре, получаваме, че системата ще открие 6 души от 10 с вероятност 0,9.
За n=10 горната граница на доверителния интервал е , което означава, че вероятността да не бъде открит е 0,206, т.е. вероятност за откриване 1-0,206=0,794.
Закръглявайки нагоре, получаваме, че системата ще открие 8 души от 10 с вероятност 0,9.
За n=25 горната граница на доверителния интервал е , което означава, че вероятността да не бъде открит е 0,088, т.е. вероятност за откриване 1-0,088=0,912.
Закръглявайки нагоре, получаваме, че системата ще открие 9 души от 10 с вероятност 0,9.
Обобщете горните изчисления за различен брой опити (5, 10, 25 опита)
A)n - брой експерименти, P - вероятност за откриване, I β - доверителен интервал.
B)за случая, когато са имали само положителен резултат
n=5, Robn.=0,6 с вероятност 90%;
n=10, Robn.=0.8 с вероятност 90%;
n=25, Robn.=0,9 с вероятност 90%.
Средно време между фалшиви аларми (фалшиви аларми)
Този параметър е взаимосвързан параметър с вероятността за откриване (Robn.). Колкото по-високо (Robn.), толкова по-малко (Tal. тревоги.).
Голям брой фалшиви аларми се отразява негативно на ефективността на защитата, тъй като операторът спира да реагира на текущи събития, считайки ги за фалшива аларма, следователно, в зависимост от важността на защитения обект и стойносттапараметър, за да бъде регистриран, е необходимо да изберете този параметър разумно.
От практиката обикновено се смята, че средното време между фалшивите аларми трябва да бъде не повече от 24 часа.
В общия случай допустимото време между фалшивите аларми се определя от изискванията на клиента, който ги определя въз основа на спецификата на обслужване от персонала и важността на обекта на защита.
Емпирично, след като сте получили приемлива вероятност Robn, без да променяте условията на теста, трябва да се уверите, че допустимият интервал от време между фалшивите аларми е приемлив.
Често при тестовете за приемане вероятността за откриване се записва при една системна настройка, а времето между фалшивите аларми се записва при други настройки. Този подход е невалиден.
Забележка.Понякога Tfl. аларма заменена от вероятността от фалшива аларма. (Rlt). В нашия случай Тлож. аларма по-интуитивен.
Вероятност за фалшива тревога. Рlt е вероятността през времето T да възникне фалшива аларма на системата. Статистически се оценява честотата на фалшивите аларми - броят на фалшивите аларми за определен период от време. Средният интервал от време между две последователни фалшиви аларми се нарича време между фалшивите аларми (False alarms). В понятието за Поасоновата природа на потока от фалшиви аларми може да се напише:
Рlt \u003d exp (Tp. / T фалшиви аларми.)
където: RLT. - вероятност от фалшива тревога;
Tp.- времето, през което системата е в работно състояние.
Разглежданите характеристики са свързани помежду си с такъв параметър като чувствителността на системата. Чувствителността е реципрочната стойност на прага. Праг - определена стойност, под която въздействието се интерпретира като шум. Прагът се настройва по време на настройката на системата. Колкото повечечувствителност, толкова по-голяма е вероятността от Pbn., но с увеличаване на чувствителността честотата на фалшивите аларми (Fl.) също се увеличава. Тази ситуация е показана на фигура 19.
Когато настройвате системата, трябва да маневрирате между тези параметри, докато задачата е да изберете оптималното ниво на чувствителност.
Често в научната литература можете да намерите термините „грешка от тип I“ и „грешка от тип II“. Тези термини са близки по същество (Robn и Rlt).
Грешки от първи вид(англ. type I errors, α errors, false positives) игрешки от втори вид(eng. type II errors, β errors, false negatives) в математическата статистика са ключовите концепции на проблемите на тестване на статистически хипотези. Въпреки това, тези концепции често се използват в други области, когато става въпрос за вземане на „двоично“ решение (да / не) въз основа на някакъв критерий (тест, проверка, измерване), което с известна вероятност може да даде грешен резултат.
Грешка тип Iчесто се наричафалшива аларма, фалшиво положително или фалшиво положително.
Грешка тип IIпонякога сенарича пропуснато събитиеили фалшиво отрицание.
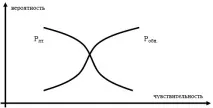
Фиг. 19 - Връзка между вероятността за откриване (Robn.) и вероятността от фалшиви аларми Rlt.