Условия за успоредност и перпендикулярност
права и равнина в пространството.
За да са успоредни права и равнина е необходимо и достатъчно нормалният вектор към равнината и насочващият вектор на правата да са перпендикулярни. За целта е необходимо тяхното скаларно произведение да е равно на нула.
За да бъдат права и равнина перпендикулярни е необходимо и достатъчно нормалният вектор към равнината и насочващият вектор на правата да са колинеарни. Това условие е изпълнено, ако кръстосаното произведение на тези вектори е равно на нула.
Повърхности от втори ред.
Дефиниция. Повърхностите от втори ред са повърхности, чиито уравнения в правоъгълна координатна система са уравнения от втори ред.
Определение. Цилиндричните повърхнини са повърхнини, образувани от линии, успоредни на някаква фиксирана права линия.
Нека разгледаме повърхнините, в уравнението на които липсва компонента z, т.е. водачите са успоредни на оста Oz. Видът на линията в равнината XOY (тази линия се нарича водеща повърхност) определя характера на цилиндричната повърхност. Разгледайте някои специални случаи в зависимост от уравнението на ръководствата:
1) - елиптичен цилиндър.
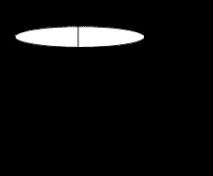 |
2) е хиперболичен цилиндър.
 |
2)x 2 = 2pyе параболичен цилиндър.
 |
Определение. Повърхност, описана от определена линия, въртяща се около фиксирана линияd, се наричаповърхност на въртене с ос на въртенеd.
Ако уравнението на повърхността в правоъгълна координатна системаизглежда като:
F(x 2 + y 2 , z) = 0, то тази повърхнина е повърхнина на въртене с ос на въртене Оz.
Аналогично: F(x 2 + z 2 , y) = 0 - повърхност на въртене с ос на въртене Оу,
F(z 2 + y 2 , x) = 0 е повърхността на въртене с оста на въртене Ox.
Нека запишем уравненията на повърхностите на въртене за някои специални случаи:
1) -елипсоид на въртене
2) -еднослоен хиперболоид на революцията
3) -двуслоен хиперболоид на революцията
4) -параболоид на революцията
Уравненията за повърхностите на въртене, разгледани по-горе, могат да бъдат записани по подобен начин, ако оста на въртене е осите Ox или Oy.
Повърхностите, изброени по-горе, обаче са само специални случаи на общи повърхности от втори ред, някои видове от които са обсъдени по-долу:
Сфера:
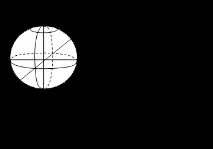 |
Триаксиален елипсоид:
При сечението на елипсоида с равнини, успоредни на координатните равнини, се получават елипси с различни оси.
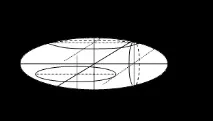 |
Еднолистов хиперболоид:
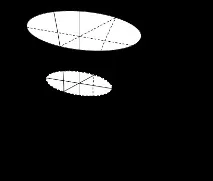 |
Двуслоен хиперболоид:
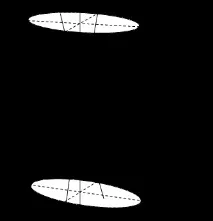 |
Елиптичен параболоид:
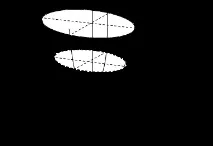 |
Хиперболичен параболоид:
 |
Конус от втори ред:
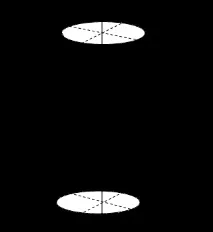 |
Цилиндрични и сферични координатни системи.
Както в равнина, в пространството позицията на всяка точка може да се определи от три координати в различни координатни системи, различни от декартовата правоъгълна система. Цилиндрични и сферични координатни системи саобобщение за пространството на полярната координатна система, което беше разгледано подробно по-горе.
Да въведем в пространството точката О и лъчаl, излизащ от точката О, както и вектора . През точка O може да се начертае една равнина, перпендикулярна на нормалния вектор.
За да се въведе съответствие между цилиндрична, сферична и декартова правоъгълна координатна система, точката O се комбинира с началото на декартовата правоъгълна координатна система, лъчътl- с положителната посока на остаx, нормалният вектор - с остаz.
Цилиндрични и сферични координатни системи се използват в случаите, когато уравнението на крива или повърхност в декартова правоъгълна координатна система изглежда доста сложно и операциите с такова уравнение изглеждат трудоемки.
Представянето на уравнения в цилиндрична и сферична система прави възможно значително опростяване на изчисленията, което ще бъде показано по-долу.

OM1 = r; MM1=h;
Ако от точката M спуснем перпендикуляра MM1 към равнината, то точката M1 ще има полярни координати (r, q) на равнината.
Определение.Цилиндричните координати на точка M са числа (r, q, h), които определят позицията на точка M в пространството.
Определение.Сферичните координати на точката M са числата (r,j,q), където j е ъгълът между r и нормалата.
Връзка между цилиндричен и декартов правоъгълник
Подобно на полярната координатна система в равнината, могат да се записват отношения, които свързват различни координатни системи в пространството. За цилиндрични и декартови правоъгълни системи тези отношения приемат формата:
h = z; x = rcosq; y=rsinq; cosq =; sinq =.