Задача номер 3 Движение на планетите

Движението на планетите. Законите на Кеплер. Паралакс.
Цел: Да овладеете техниката за решаване на проблеми, използвайки законите на планетарното движение.
Указания:Задачата трябва да започне след изучаване на гл.2, 3 §63-68, гл.10 [2], гл.10 [1].
Изходните данни и основната информация за изпълнение на задача №3 са дадени в Приложение №3.
1. Колко често се повтарят опозиции за планета, чийто звезден период е известен?
2. Изчислете масата на планетата, като знаете звездния период на нейния спътник и разстоянието на спътника от планетата.
3. Колко време е необходимо на една планета да направи пълна обиколка около Слънцето, ако е известно разстоянието й от него?
4. Определете разстоянието до небесно тяло, ако е известен неговият хоризонтален паралакс.
5. Изчислете параболичната скорост на повърхността на спътника, като знаете неговия радиус и съотношението на масата на планетата към масата на спътника.
Общи сведения от теорията
Планетите се движат около слънцето по елиптични орбити. Удължението на орбитите е малко и при решаването на много задачи планетарните орбити могат да се считат за кръгови и лежащи в равнината на еклиптиката. Характерните взаимни позиции на планетите спрямо Слънцето и Земята се наричат планетни конфигурации. Планетите, чиито орбити са разположени вътре в орбитата на Земята, се наричат долни, а планетите, чиито орбити са разположени извън орбитата на Земята, се наричат горни. Конфигурациите на горната и долната планета са различни и са показани на фиг. (3.1), на който с буквата Т е отбелязано положението на Земята и са изписани имената на конфигурациите. Долните планети се наблюдават най-добре в близост до елонгации - най-голямото видимо ъглово разстояние на планетата от Слънцето. Горните планети се виждат най-добре отблизо.конфронтации, когато цялото полукълбо на планетата, осветено от Слънцето, е обърнато към Земята.
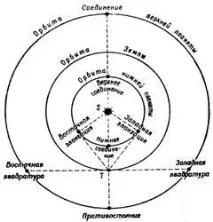 |
Ориз. 3.1. Планетарни конфигурации
Периодът от време, през който планетата прави пълно въртене около Слънцето в орбита спрямо звездите, се наричасидеричен(илизвезден) период на въртене (T), а периодът от време между две идентични планетарни конфигурации се наричасинодиченпериод (S). Планетите се движат около Слънцето в една и съща посока и всяка от тях след период от време, равен на сидеричния период, прави едно пълно завъртане.
След период от време, равен например на звездния период на Земята (ТÄ), долната планета ще изпревари Земята, а горната ще изостане от нея, т.е. първоначалната конфигурация на планетите няма да бъде възстановена. Следователно синодичният период не е равен на звездния. За долната планета, която обикаля по-бързо от Земята, можем да напишем
, (3.1)
и за горната, която се движи по-бавно от Земята, -
, (3.2)
където TÄ=1 година (или 365,26 дни).
Формули (3.1) и (3.2) се наричат уравнения на синодичното движение.
Планетите се движат около Слънцето споредзаконите на Кеплер:
1. Орбитата на всяка планета е елипса, в един от фокусите на която е Слънцето.
2. Радиус – векторът на планетата за равни периоди от време описва равни площи.
3. Квадратите на звездните периоди на две планети са свързани като кубовете на големите полуоси на техните орбити,
(3.4)
(3,5)
Тези закони са валидни и за движението на спътниците около техните планети.
Законите за движение на небесните тела са резултат от тяхното взаимодействие споредзакона за всемирното привличане -всички тела се привличат едно към друго ссила, чийто модул е право пропорционален на произведението на техните маси и обратно пропорционален на квадрата на разстоянието между тях.
Законът за всемирното притегляне се изразява с формулата:
, (3.6)
къдетоm1 иm2 са масите на телата;r– разстояние между центровете им;f- универсална гравитационна константа (нейната SI стойностf=6,67*10-11 m/kg s2). Нютон извежда законите на Кеплер от закона за всемирното привличане.
Под въздействието на гравитацията едно небесно тяло може да се движи спрямо друго по крива на конично сечение - по окръжност, елипса, парабола и хипербола. Това епървият обобщен закон на Кеплер. За да се определят масите на небесните тела,обобщаването на третия закон на Кеплерза всяка система от циркулиращи тела е от голямо значение.
Квадратите на звездните периоди на планетите (T12 и T22), умножени по сумата от масите на Слънцето и планетата (M¤+m1 и M¤+m2), се отнасят като кубове на големите полуоси на орбитите на планетите (a13 и a23).
Обобщеният трети закон на Кеплер е приложим и към други системи, като например движението на планета около Слънцето и спътник около планета.
За да направите това, движението на Луната около Земята се сравнява с движението на спътник около планетата, чиято маса се определя, като в същото време масите на спътниците се пренебрегват в сравнение с масата на централното тяло. Тогава масата на планетата Mn се изчислява по формулата:
, (3.8)
където T1 и 1 са периодът на въртене и голямата полуос на орбитата на спътника на планетата.
СкоросттаV, когато тяло с масаmсе движи под въздействието на гравитацията по орбита с голяма полуос на разстояниеrот централното тяло, се намира по формулата:
, (3,9)
къдетоMе масата на централното тяло.
Акоmе значително по-малко отM, тогава може да се приеме за нула във формулата. ОбозначетеfMпрезm..
Когато тялото се движи в кръг (r=)от уравнение (3.9) следва
, (3.10)
къдетоVkе кръговата скорост.
Когато тялото се движи по парабола (=¥), от уравнение (3.9) следва
, (3.11)
къдетоVP– параболична скорост.
Скоростта на елипсовидно движение VE е в границите