1.2. Алгоритъм на Метрополис
Целта на алгоритъма на Metropolis е да създаде такава последователност от състояния a1, a2, . am такова, че разпределението става Болцманово в границата m → ∞.
По-подробна информация за веригите на Марков може да бъде получена например в [15], [6]. Нека сега формулираме самия алгоритъм на Metropolis. Вероятността P(b ← a) за приемане на пробно движение, което трансформира системата от състояние a в състояние b, е дадена, както следва:
,
Може да се покаже, че условието за подробен баланс е изпълнено и разпределението на състояниятаa1,a2, . във фазовото пространство се дава от функциятаp(R). Така преходът се осъществява в едно от състояниятаaилиb, което има голяма вероятност.
Следващата итерация на алгоритъма започва от състоянието и е както следва:
изберетеx' по разпределение;
;
С вероятностa(1 акоa>1) , в противен случай.
Изводът е, че се преместваме в нов разпределителен център, ако направим следващата стъпка, и получаваме произволна разходка, която зависи от разпределениетоp: винаги правим стъпка, ако функцията на плътност нараства в тази посока и понякога я отхвърляме, ако намалява (отхвърляме не винаги, защото трябва да можем да излезем от локалните максимуми и да се лутаме под цялата графикаp). Отбелязвам, между другото, че когато една стъпка е отхвърлена, ние не просто отхвърляме нова точка, но повтаряме същото нещоx(t) втори път - по този начин има голяма вероятност за повтаряне на проби около локалните максимуми на разпределениетоp, което съответства на по-висока плътност (фиг. 1).
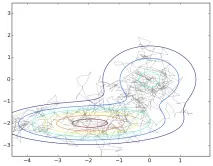
Ориз. 1. Скитане в равнина под графика на смес от две двумерни гаусиани
Глава 2 Прилагане на алгоритъма Metropolis
За да организираме компютърен експеримент, използвамепрограма, написана на Pascal.
2.1. Софтуерна реализация на алгоритъма
Тяло, ограничено до две функции и
.Решението за този пример е обемът на даденото тяло.
За опростяване на изчисленията ограничаваме областта на интеграция:
Формира се триизмерен масив, изпълнен със стойностите 1/n, където n е общият брой точки.
Точка се избира произволно в зоната на ограничение, след което тази точка се проверява за принадлежност към фигура, ограничена от функции и, ако точката принадлежи, тогава 1 се записва в масива при координатиx,y,z, ако не, тогаваp(b)/p(a).
Броят на принадлежащите точки се отчита от брояч и обемът на фигурата се изчислява по метода Монте Карло.
2.3. Анализ на резултатите от експеримента
По време на експеримента направихме стъпка равна на 0,001, 0,0002 и 0,0001. При всяко стартиране на програмата се генерират 1000, 5000 и 10000 произволни точки. Резултатите от тестването на програмата са представени в таблица 1.