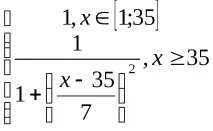1.3 Езикови променливи
Езиковите променливи се използват за описание на задачи за вземане на решения. L. Zadeh въвежда концепцията залингвистична променлива(лингвистична променлива)[98], чиито стойности са думи и/или изречения на естествен език, които се описват с размити стойности.
Набор от термини(набор от термини)е набор от всички възможни стойности на лингвистична променлива.
Термин(термин)е всеки елемент от набор от термини. В теорията на размитите множества терминът се формализира от размито множество, използвайки функция на принадлежност.
Например, лингвистичната променливаAGEприема размити стойности "млад", "млад", "среден", "стар", "стар",и т.н., които са термини, които образуват набор от термини. В предишния пример термините бяха стойностите "нисък", "среден", "висок" на лингвистичната променлива "ръст на мъж".
Пример.Да разгледаме лингвистична променлива с имеx= "стайна температура". Тогава универсалното множествоU=[5; 35]; набор от терминиT= с функции на принадлежност
μ"студено"=
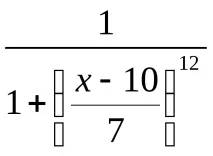
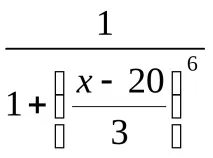
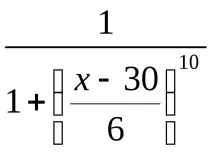
Синтактичните правила, които генерират нови термини с помощта на кванторите „не“, „много“ и „повече или по-малко“, са дадени в таблица. 5.
Правила за изчисляване на функции на принадлежност
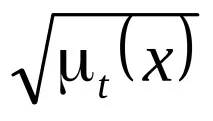
Графиките на функциите на принадлежност на термините "студено", "не много студено", "удобно", "повече или по-малко удобно", "горещо" и "много горещо" на лингвистичната променлива "стайна температура" са показани на фиг. 7.
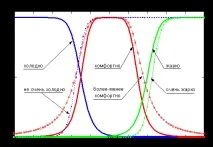
Ориз. 7. Езикова променлива "стайна температура"
Езиковите променливи могат да бъдат числови или нечислови. Числовите променливи съответстват на размитите числа.
Ако кардиналността на набора от носители е
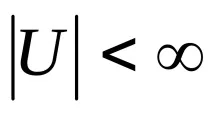
Ако кардиналността на набора от носителиконтинууме
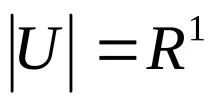
Например скоростта е числова лингвистична променлива, сложността е нечислова лингвистична променлива (стойностите са „ниски“, „средни“, „умерени“, „високи“).
Нека разгледамекритерия за растеж на печалбатакато лингвистичен със стойности на скалата на растежа "нисък", "среден", "висок" и числова област на дефиницияU=[1,10] милиона рубли.
На фиг. 8 показва областите на членство на размити множества, които характеризират посочените стойности на лингвистичния критерий. "нисък" (2) показва субективна оценка на това как цифровата стойност на растежа на печалбата, равна на 2 милиона рубли, съответства на мащабната лингвистична стойност "нисък растеж".
"нисък" "среден" "висок"
1 2 3 4 5 6 7 8 9 10 милиона рубли
Ориз. 8. Стойности на лингвистичния критерий "увеличаване на печалбата" и съответните функции на членство
Езиковите критерии, както и съответните лингвистични променливи, могат да бъдат числови и нечислови.
Разглежданият критерий "увеличаване на печалбата" е непрекъсната числова лингвистична променлива. И пример за нечислов лингвистичен критерий е критерият за „професионална пригодност“, който има значенията „добър“, „лош“, „не пасва достатъчно добре“.
Примери за размити множества
НекаX=,M=[0,1]. Размитото множество "няколко"може да се дефинира по следния начин:
НекаХ=0,1,2,3.n.>.Размитият набор "малък" може да се дефинира, както следва, използвайкифункции на членство:supp"small"=>, тук функцията на членство на елементnв размит набор "small" е
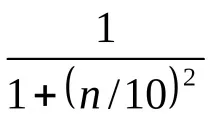
НекаХ= и съответства на понятието "възраст", тогава размитото множество "млад" може да бъде определено с помощта на функцията за членство
“млад”(x) =