4.3. Конгруентна трансформация
Казват, че две матрици са конгруентни, ако съществува неособена матрица Q, която удовлетворява равенството
5. Собствени стойности, собствени вектори и диагонализация на матрици
5.1. Собствени стойности и собствени вектори на матрица
Да предположим, че сред безкрайното множество от едномерни пространства R1 има такива, които ще бъдат инвариантни спрямо трансформацията y=Ax, тоест за всеки xR1. Означаваме с отношението на y към x, което в този случай ще бъде просто реално число, тоест можем да напишем y=x. Така, ако R1 е инвариантно подпространство, тогава xR1 удовлетворява равенството
Векторът x0, който удовлетворява тази връзка, се нарича собствен вектор на матрицата A, а числото се нарича собствена стойност на матрицата A.
За да определим характеристичните числа на матрицата, пренаписваме тази връзка в различна форма, като въвеждаме идентичното преобразуване x=Ix. В същото време получаваме
Тази връзка е система от линейни еднородни уравнения. За да има тази система нетривиално решение, е необходимо и достатъчно det (A–I)=0. В този случай самите променливи, тоест векторът x, се определят с точност до постоянен фактор. Съотношението det (A–I)=0 се нарича характеристично уравнение на матрицата A, което е алгебрично уравнение от n-та степен по отношение на . Това уравнение има n корена, сред които може да има еднакви, които са собствени стойности на матрицата A.
Замествайки всяка собствена стойност i в оригиналната система от уравнения, получаваме уравнението
който има нетривиално решение. Това решение дава вектор xi, дефиниран до скаларен фактор. Този вектор се нарича характерен вектор на матрицата A.
5.2. Диагонализация на матрици.
За матрица А,имайки n различни характерни числа, трансформация на формата M-1AM води до диагонална матрица D, където M се нарича модална матрица. Матрицата M е съставена от характеристичните вектори на матрицата A.
Въпреки това, матрица с обща форма с размерност (nn) с множество характеристични числа може да съдържа по-малко от n линейно независими характеристични вектора; следователно може да не е възможно да се преобразува в диагонална форма чрез трансформация. Въпреки това може да се покаже, че произволна квадратна матрица може да бъде редуцирана чрез трансформация на подобие до канонична Йорданова матрица със следните свойства:
Диагоналните елементи на тази матрица са характерните числа на A.
Всички елементи под главния диагонал са равни на нула.
Ако съседните елементи на главния диагонал са еднакви, тогава елементите непосредствено вдясно от главния диагонал са равни на единица. Типична форма на Джордан е:
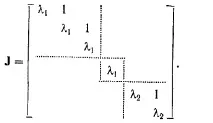
Имайте предвид, че единиците се срещат в блокове на формуляра

Те се наричат Йорданови клетки.
Броят на Джорданови клетки, свързани с дадено характеристично число i, според трансформацията на подобие, водеща до формата на Джардан, е равен на броя на собствените вектори, свързани с характеристичното число, тоест q-дефектът [iI–A]. Не е лесно обаче да се определят редовете на клетките на Йордан. Следователно не е ясно дали трансформацията J=M-1AM води до горната Йорданова форма или формата
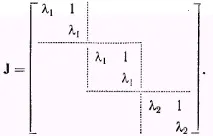
Полезно е да знаете, че в случай на пълно израждане няма да има настоящи 1. В случай на просто израждане (q=1), всички елементи непосредствено вдясно от главния диагонал са равни на единица. За случаи, които не се вписват в горното, е необходимоизползвайте метода на пробата и грешката, основан на равенството, за да определите J и M
Нека колоните на M бъдат означени с x1, x2, …, xn. Тогава има Йорданова клетка от ред m, свързана с I само ако m линейно независими вектора x1, x2, …, xm удовлетворяват уравненията:
Тези изрази се отнасят за всяка клетка на Jordan.