5.6 Обратно проследяване
5.6.1 Въведение
Има клас алгоритми, наречениbacktrackingalgorithms,което означава „алгоритми за обратно проследяване“. По правило такива алгоритми се основават на рекурсия. Тези алгоритми се различават по това, че търсят решение чрез проба и грешка, преминавайки през всички или почти всички опции. Алгоритмите с обратно проследяване могат да бъдат наречени "челно"; има много по-напреднали класове алгоритми (динамично програмиране, разделяй и владей, алчни алгоритми). Тези. когато трябва да се справите със задачата да намерите оптималното решение, когато е невъзможно да приложите някой от известните методи, които могат да намерят оптималното решение, и остава да се прибегне до последното средство - изчерпателно изброяване.
Тази ситуация възниква в следните случаи:
Търсете оптималното с пълно изброяване на всички опции;
Търсете всяко решение с изход, когато бъде намерено;
Търсете оптималното решение с изчерпателна оптимизация на изброяването (отрязване на опции, които очевидно са по-лоши от оптималното решение, намерено до този момент).
5.6.2 Алгоритми за търсене
Помислете за алгоритми за изброяване, базирани на методи за обхождане на графика, като използвате проблема за намиране на най-краткия път в лабиринт като пример. Тъй като има два метода за обхождане на графиката, ще разгледаме два алгоритъма за изброяване.
Лабиринтът, състоящ се от проходими и непроходими клетки, е даден отAматрицаmn. Матричен елементA[i,j]=0, ако клетка (i,j) е проходима. В противен случайA[i,j]=.
Изисква се да се намери най-краткият път от клетка (1, 1) до клетка (m,n).
Всъщност е дадена обърната матрица на съседство (където нулите са заменени с , а единиците са заменени с нули). лабиринте графика.
Методът за обратно проследяване (наричанbacktrackingна английски) се основава на метода за търсене в дълбочина. Обратното проследяване е метод на проба и грешка („нека се опитаме да тръгнем в тази посока: ако не се получи, нека се върнем и опитаме в друга“). Тъй като говорим за итерационни опции с помощта на метода за първо търсене в дълбочина, по време на работа на алгоритъма е необходимо текущият път да се съхранява в дървото. Този път е стек от Way. Освен това е необходим масив Dest, чиято размерност съответства на броя на върховете на графа, съхранявайки за всеки връх разстоянието от него до оригиналния връх.
Да се върнем към нашата задача. Нека някоя клетка е текуща (в началото на алгоритъма, клетка (1, 1)).
ако текущата клетка има съседна клетка Neighbor, така че:
(не по пътя) и
(Dist[Neighbor]=0 или (Dist[Neighbor] > Length(Way))) след това започнете
добавете Neighbor към Way;
текуща клетка := съсед;
Списък 5.15 - Алгоритъм за итеративен лабиринт
От горния фрагмент става ясно защо този метод се нарича обратно проследяване. Връщането тук съответства на операцията "изтегляне от пътя", която намалява дължината на пътя с 1.
Изброяването приключва, когато Way е празен и се направи опит за връщане обратно. При това положение няма къде да се върне.
Way е текущият път, но в процеса на работа е необходимо да се съхрани и оптималният OptimalWay път.
Имайте предвид, че алгоритъмът може да бъде подобрен, като не се позволява дължината на Way да бъде по-голяма или равна на дължината на OptimalWay. В този случай, ако се намери някакъв вариант с по-голяма дължина, той със сигурност няма да е оптимален. Такова подобрение обикновено означава, че веднага щом текущият път стане очевидно неоптимален, човек трябва да се върнеобратно. В някои случаи това подобрение на алгоритъма може значително да намали изброяването.

Фигура 5.14 - Търсене на изход от лабиринта с помощта на метода за търсене в дълбочина
Алгоритъмът за търсене в ширина се състои от две стъпки:
Разпространението на вълната е самото търсене в ширина, при което клетките се маркират с номера на стъпката на метода, при който клетката е посетена. При обратното движение, започвайки от крайния връх, се възстановява най-късият път, по който е достигнат чрез включване на клетки с минимален знак в него. Важно е възстановяването да започне от края (от началото често е невъзможно).
Трябва да се каже, че търсенето в ширина, в сравнение с обратно проследяване, обикновено изисква повече допълнителна памет, която се изразходва за съхраняване на информация, необходима за изграждане на път при обратно движение и маркиране на посетени върхове, но също така работи по-бързо, тъй като посещението на една и съща клетка повече от веднъж е напълно изключено.

Фигура 5.15 - Намиране на изход от лабиринта с помощта на търсене в ширина
Като друг пример, помислете за игри с двама души, които обикновено се описват с набор от „позиции“ и набор от правила за преминаване от една позиция в друга, като се предполага, че играчите се редуват в движението. Предполагаме, че само крайни последователности от позиции са разрешени от правилата и че всяка позиция има само краен брой разрешени ходове. След това за всяка позицияpима числоN(p), така че никоя игра, започнала приp, не може да продължи повече отN(p) хода.
Крайните позиции са позиции, от които няма законни ходове. На всеки от тях е дефинирана целочислена функцияf(p), която определя изплащането на един отиграчът, който притежава хода в тази позиция; печалбата на втория играч се счита за равна на -f(p).
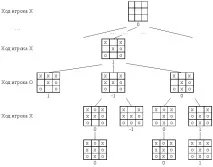
Фигура 5.16 - Дърво на играта Tic-tac-toe
Ако имаdзаконни ходовеp1, …, pdот позицияp, тогава възниква проблемът с избора на най-добрия. Ще наречем даден ход най-добър, ако в края на играта той носи възможно най-голяма печалба, при условие че противникът избира ходовете, които са най-добри за него (в същия смисъл). Некаf(p) е най-голямата печалба, постижима в позицияpот играча, който притежава хода на хода срещу оптимална защита. Тъй като след преместване на позицияpiпечалбата на този играч е -f(pi),имаме
Тази формула ви позволява да дефинирате индуктивноf(p) за всяка позицияp.
Следният алгоритъм, наречен обратно проследяване, оценяваf(p).