Част I
Да предположим, че в играта, която разработваме, играчът стреля с пистолет по противник. Как да определите дали куршум, изстрелян от дадена точка в определена посока, е уцелил целта? Един възможен подход е да се симулира траекторията на куршум с лъч и да се моделира врагът сограничаваща сфера(ограничаваща сфера). (Ограничаващата сфера е просто сфера с най-малък диаметър, която пасва на целия обект, което дава приблизително представяне на обема, който заема. Ще говорим повече за ограничаващите сфери в глава 11.) След това, използвайки математически изчисления, можем да определим дали лъчът пресича сферата и, ако е така, къде. В този раздел ще обсъдим математическия модел на лъчите.
Един лъч се описва чрез определяне на начална точка и посока. Формулата на параметричния лъч изглежда така:
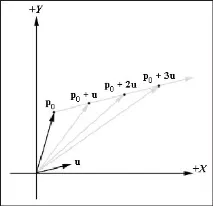 |
Ориз. 14. Лъч, определен от начална точкаp0 и вектор на посокатаu. Можем да генерираме лъчеви точки, като заместваме различни стойности на t във формулата, която трябва да бъде по-голяма или равна на нула
Във формулата на лъча p 0 е началната точка, u е векторът, който определя посоката на лъча, аtе параметърът. Чрез заместване на различни стойности наtможем да получим координатите на различни точки на лъча. Освен това за лъча стойносттаtтрябва да бъде в диапазона [0, ∞). Стойности по-малки от нула ще доведат до изчисляване на координатите на точките зад лъча (на линията, от която лъчът е част). Всъщност, акоtприема стойности от диапазона (–∞, ∞), получаваме линия в триизмерното пространство.
Пресечна точка на лъч и равнина
Да предположим, че имаме лъч p (t) = p 0 +tu и равнина n × p +d= 0 и искамеопределете дали лъчът пресича равнината и ако е така, изчислете координатите на пресечната точка. За да направим това, поставяме формулата на лъча във формулата на равнината и изчисляваме стойността на параметъраt, който удовлетворява уравнението на равнината. Заместването на намерената стойност в уравнението на лъча ви позволява да изчислите координатите на пресечната точка.
Заменяме формула (9) във формулата на равнината:
Заместете уравнението на лъча във формулата на равнината.
Извадете променливата от скобите.
Ако стойносттаtне е в диапазона [0, ∞), тогава лъчът не пресича равнината.
Ако стойносттаtе в диапазона [0, ∞), пресечната точка се намира чрез заместване на намерената стойност на параметъра във формулата на лъча: