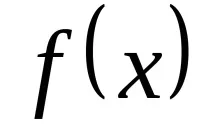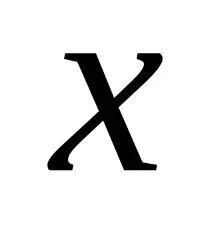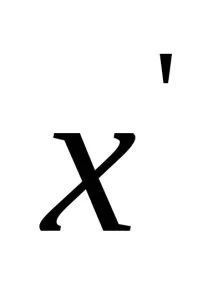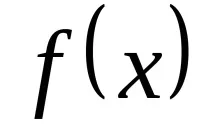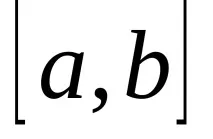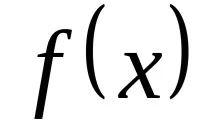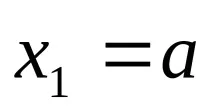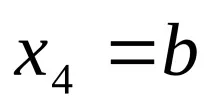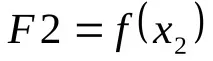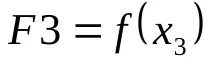Едноизмерна оптимизация
Български химикотехнологичен университет Д. И. Менделеев
Катедра по изчислителна математика
Методи за едномерна оптимизация
Изпълнено от: Павлов В.А. гр. I-24
Проверен от: Epishkin A.P.
Методи за едномерна оптимизация
За дадена функция
на една променлива
е необходимо да се определи стойност
, при която функцията
приема екстремна стойност. Обикновено се разбира като минимална или максимална стойност. Като цяло, една функция може да има една или повече крайни точки. Намирането на тези точки със зададена точност може да се раздели на два етапа. Първо се разделят екстремните точки, т.е. определят се сегменти, които съдържат по една крайна точка, след което се прецизират до необходимата точност
. Разделянето може да се извърши както графично, така и таблично. Всички методи за уточняване на екстремна точка ще бъдат разгледани по отношение на минималното уточняване на даден интервал.
Метод на разделяне на три равни сегмента.
1. Дадена е отсечка
, на която са определени функцията
и точността
. Необходимо е да се посочи минималната точка с определена точност. Нека въведем нова нотация за точките
и
. И изчислете Z=1/3.
2. Разделете отсечката на три равни части и определете точка и точка. Ние изчисляваме стойностите на функцията в тези точки
,
.
3. Дефинираме нов сегмент, съдържащ екстремалната точка, като сравняваме стойностите на функциите F2 и F3. Ако F2 Съседни файлове в папка Word