Хорст Файстел

Хорст Файстел. Криптография и компютърна сигурност. Превод А. Винокуров. Част 3

Читателят може да бъде изненадан и ужасен да научи, че класът на шифър на Vernam – единственият клас на шифър, който може да бъде доказано неразбиваем в абсолютния смисъл на термина – е недостатъчен в друг смисъл: той сам по себе си не осигурява защита срещу хитроумни измами с неизлишен трафик.

Независимо от това дали съобщението е кодирано с помощта на истински случайни цифри или псевдослучайна последователност от цифри, при такова битово криптиране, една грешка, възникнала по време на предаване на съобщението, остава в рамките на една позиция на цифрата; грешката не се "разпространява", не се разпространява в останалата част от съобщението. Този шифър не въвежда междусимволни зависимости. Когато едно съобщение е написано на естествен език като английски, контекстът на естественото излишък улеснява лицето, което чете текста, да забележи случайни грешки. По този начин, ако някои от 5-те бита, представляващи буквата E, бяха повредени по такъв начин, че съответната група от битове се превърна в представяне на буквата F (така, например, че думата SECRET стана SECRFT), тогава човешкият читател веднага ще открие грешката.

Ситуацията е съвсем различна при използването на компютри. Предадените тук данни може да не съдържат излишък, например, ако са изцяло цифрови и в тази ситуация грешка само в една цифра може да причини цяла каскада от изчислителни грешки. Проучването на проблема показа, че простите кодове за откриване на грешки не са подходящи за защита на целостта на компютърните данни от евентуална манипулация от човешки експерти. В тази ситуация е необходимо не само да се откриват грешки, но и да се защити с криптографияметоди за удостоверяване. Изненадващо, това се постига най-добре чрез базиране на решението на определени принципи, присъщи на структурите за криптиране. Вместо да се опитваме да променим концепцията за поток, нека погледнем наново концепцията на цялата криптография: замяна на блокове или цифри на съобщение.

Ще наричаме всеки шифър, който преобразува n цифри от съобщение в n цифри от шифрован текст, блоков шифър. Например, блоков шифър би бил този, който преобразува кода 00000, който според нашата конвенция представлява буквата A в обикновен текст, в, да речем, 11001, еквивалентът на шифрован текст на A, даден ключ за пермутация, точно както е посочено от таблицата за заместване. За да видите как такова двоично преобразуване се извършва от електронно устройство, нека разгледаме заместванията само в групи от три двоични цифри, както е показано на следващата фигура.

влизане изход

000	011
001	111
010	000
011	110
100	010
101	100
110	101
111	001

Блокът за заместване, за разлика от поточните устройства, е по-общ по природа и включва както линейни, така и нелинейни трансформации: той не просто добавя нули и единици към входните цифри, но може да замени всеки входен блок от цифри с всеки изходен блок. В действителност той се състои от два превключвателя - единият преобразува двоично число от n цифри в една цифра с основа 2 n, а другият извършва обратното преобразуване. По този начин блокът съдържа 2 n вътрешни превключвателни връзки, които могат да бъдат направени 2 n! различни начини. Това означава, че вВ случая на блока, показан на тази фигура с n = 3, има 40320 различни опции за окабеляване или таблици, подобни на тази, показана на фигурата. Блок от този тип с n = 128 би направил анализа практически невъзможен, но е технологично невъзможен за създаване.

Осем елемента могат да бъдат представени с помощта на три двоични цифри: 2 3 е равно на осем. Заместващото устройство се състои от два превключвателя. Първият преобразува поредица от три двоични цифри в съответната осмична стойност, като подава сигнал към точно един от осемте изходни реда. Тези осем изхода могат да бъдат свързани към осемте входа на втория превключвател с всеки от 8-те! или 40320 начина. Ние сме свободни да изберем коя от 40320 различни опции за свързване или превключване на проводници между първия и втория суич да използваме. Ролята на втория превключвател е да преобразува входа, представен от една единствена базова 8 цифра, обратно в трицифрен двоичен изход.

Ако беше създадено устройство за заместване, което да обработва петцифрен двоичен вход, то можеше да се използва за криптиране на азбука от 32 знака. Тогава броят на възможните връзки на два комутатора ще бъде 32!. Това може да изглежда като невероятно голям брой ключове, но така създаденият шифър все още трябва да се третира като много слаб: той не може да издържи на честотен анализ. Тази слабост не му е присъща; описаното математически устройство дефинира най-общата възможна трансформация. Той включва, за всеки даден входно-изходен размер, всеки възможен обратим шифър, който някога е бил или дори може да бъде изобретен; математиците биха могли да кажат, че представлява пълната симетрична група. Тойнапълно "несистематично": едно свързване на превключватели не казва нищо на опонента за всички останали връзки. Слабостта не е присъщо свойство на шифъра, тя се дължи на избрания размер на блока. Въпреки големия брой ключове, "каталогът" на възможните входове или изходи е много малък: има само 32 елемента в него. Това, което е необходимо тук, е толкова голям каталог, че би било почти невъзможно за всеки противник да го запише. Ако, например, имаме блок със 128 входа и изхода, анализаторът ще трябва да преодолее 2128 (или повече от 1038) възможни блока от числа - толкова огромно число, че честотният анализ тук просто не е осъществим. За съжаление, заместващо устройство със 128 входа също би изисквало 2128 вътрешни връзки между първия и втория комутатор, което не е технологично осъществимо. Това е основната дилема на криптографията. Знаем какъв е идеалът, но не можем да го постигнем на практика.

Има обаче трансформация, която е лесна за изпълнение за голям набор от входове. Практически е възможно, например, да се изгради блок с, да речем, 128 входни и изходни пина, които са вътрешно свързани с обикновени проводници, както е показано на следващата фигура. За такъв "блок от пермутации" с n изхода има n! възможни опции за превключване на проводници, всеки от които се определя от отделен ключ. Може лесно да се изгради за n = 128. Въпреки че това ще ни предостави голям брой възможни ключове (128!), което е доста полезно, сега се натъкваме на нова трудност. Чрез използване на набор от специално конструирани съобщения е възможно напълно да се определи ключът на такава система само с n -1 (в този случай 127) опита. Този трик е да използвате поредица от съобщения, съдържащи едноединична единица в n -1 различни позиции; позицията на един в изходния блок ще "даде" кабелната връзка, използвана в устройството. Слабостта на простия пермутационен блок е, че той отново е линейна система.

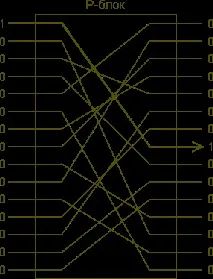Блокът за пермутация може да "обслужва" много редове, но променя само позицията на числата. Опонентът може да научи вътрешната си комутация, като му даде единични като вход и наблюдава на кой изход се появяват тези.

Нуждаем се от компромис, който поне да се доближи до характеристиките на цялостната система. Дойдохме с идеята за съставен шифър, в който два или повече шифъра се комбинират по такъв начин, че получената система да е по-сигурна от която и да е от съставните й системи, взети отделно. Точно преди Първата световна война бяха изследвани различни тромави шифри, използващи множество стъпки за криптиране. Първият наистина успешен пример вероятно е изобретената от германците система, известна като ADFCVX система. Тук трябва само да отбележим, че тя комбинира "фрагменти" с "пермутации". При тази процедура съобщението беше разделено на сегменти и тези сегменти бяха пренаредени на други места. Важен факт, който трябва да се отбележи, е, че съставен шифър, съставен от блокови шифри, отново е блоков шифър; целта тук, разбира се, е шифърът да се държи колкото е възможно повече като общ заместващ шифър.

Между Първата и Втората световна война интересът към сложните шифри почти напълно изчезна поради успешното развитие на ротационни или жични дискови машини, които принадлежат към общия клас генератори на псевдослучайни последователности. Типична ротационна машина имашеклавиатура, която прилича на клавиатура на пишеща машина. Всяка буква беше криптирана с помощта на няколко диска, работещи в определена последователност, за следващата криптирана буква дисковете бяха преместени на различна позиция с помощта на неправилен и зависим от ключ алгоритъм. Съобщението беше декриптирано от идентична машина с абсолютно същия ключ.

Начинът, по който трябва да се комбинират принципите на разместване и разпръскване, за да се получи криптографска сила, може да бъде описан по следния начин: Видяхме, че общите пермутации не могат да бъдат реализирани за големи стойности на n, да речем n = 128, и следователно трябва да се ограничим до схеми за заместване с практически размер. В системата, разработена в IBM и наречена "Lucifer", ние избрахме n = 4 за блокове за заместване. Въпреки че това може да изглежда като много малко число, това заместване може да бъде доста ефективно, ако ключът за заместване или схемата на свързване са избрани правилно. В Lucifer нелинейното заместване ефективно осигурява определена степен на смесване.

Видяхме също, че е лесно да се конструира линеен пермутационен блок дори за n = 128. Броят на входните и изходните терминали е n. Като чисто разбъркване на цифри, устройство, което просто премества цифри от място на място, без да променя броя на 1s и 0s, блокът за пермутация е естествен разпространител на разбъркване, така че може да осигури оптимална дисперсия.