Използване на вградени функции rkfixed( ), Rkadapt( ), Bulstoer( )
Алтернативен метод за решаване на ODE е използването на вградените функции rkfixed(), Rkadapt() или Bulstoer(). Този метод донякъде губи от първия както по отношение на простотата, така и по отношение на яснотата, но понякога е необходимо да се решават ODE с алтернативен метод, например при следните обстоятелства:
- ODE се решава в контекста на по-сложни проблеми, които включват системи от диференциални уравнения (за които изчислителната единица не е приложима) - в този случай може да се изисква единен стил на програмиране;
- за предпочитане е отговорът да се получи под формата на матрица, а не на функция;
- старите версии на Mathcad нямаха изчислителна единица и потребителят има много документи, създадени по алтернативен метод.
Нека дадем пример за използване на функцията rkfixed() за решаване на същия проблем на Коши за ODE от първи ред y' =y-y 2 . Тук е необходимо изрично да се зададе началната стойност y:=0.01, да се опише първата производна D(t,y):=y-y 2 и да се посочи броят на интеграционните точки m=100. Резултатът се получава под формата на матрица y с размери (m + 1) x 2. Първата колона съдържа стойностите на аргумента t в диапазона от 0 до 10, втората колона съдържа стойностите на желаната функция y(t), фиг. 5.2.
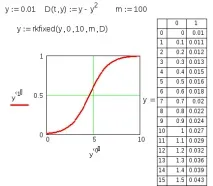
Ориз. 5.2. Решение на задачата на Коши за ОДУ от първи ред по втория начин
Това не е най-добрият стил за решаване на проблема на Коши. Наистина, първо скаларната стойност y=0,01 се присвоява на променливата y, а след това стойността на матрицата (резултатът от решаването на ODE) се присвоява на същата променлива. Този стил трябва да се избягва, когато един и същ идентификатор се използва за различни типове данни. Добро решение би било да наречете резултата по друг начин, като u.
Разглежданият пример е взет от областта на математическата екология и описва динамиката на популациите свътревидова конкуренция. Първо населението расте, близко до експоненциално, а след това се достига до стационарно състояние.
Ода от най-висок клас
Обикновено диференциално уравнение с неизвестна функция y(t), което включва производни на тази функция до y ( n ) (t), се нарича ODE от n-ти ред. Ако има такова уравнение, тогава за правилната формулировка на проблема на Коши, освен самото уравнение, е необходимо да се зададат n начални условия за самата функция y(t) и нейните производни от първи до (n -1) ред включително. В Mathcad можете да решавате ODE от по-висок ред както с помощта на изчислителния блок Given-Odesolve(), така и с алтернативен метод, използващ функции от типа rkfixed().
Вътре в изчислителния блок Given-Odesolve():
- ODE трябва да бъде линеен по отношение на най-високата производна;
- началните условия трябва да имат формата y(t0)=b или y ( n ) (t0)=b;
В противен случай решението на ODE от по-висок ред не се различава от решението на уравнения от първи ред.
На фиг. Фигура 5.3 показва решението на диференциално уравнение от втори ред за затихващ хармоничен осцилатор, което описва, например, трептенията на махало. За модела на махалото функцията Y (t) описва промените в ъгъла на неговото отклонение от вертикалната, y '(t) е ъгловата скорост на махалото, y "(t) е съответно ускорението, а първоначалните условия 0.
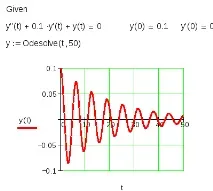
Ориз. 5.3. Решение на диференциално уравнение от втори ред
Алтернативен метод за решаване на ODE от по-висок ред се реализира с помощта на три вградени функции, които позволяват решаване на проблема във формата на Коши чрез различни числени методи:
- rkфиксиран (y, t0, t1, m, D) -метод на Runge-Kutta с фиксирана стъпка;
- Rkadapt(y, t0, t1, m, D) - метод на Рунге-Кута с променлива стъпка;
- Bulstoer(y, t0, t1, m, D) - метод на Bulirsch-Stoer;
- y - вектор на началните стойности в точка t0 с размерност n x1;
- t0 - начална точка на интервала;
- t1 - крайната точка на интервала;
- m е броят на стъпките, при които численият метод намира решение;
- D - векторна функция на диференциални уравнения с размер n x1 от два аргумента - скалар t, по отношение на който се вземат производни, и вектор y, чиито елементи са долни производни на търсената функция.
Нека покажем на примера на диференциално уравнение от трети ред
методът за формиране на векторната функция D(t,y). За целта е необходимо да се реши уравнението по отношение на най-високата производна
Тогава в това уравнение производните трябва да бъдат заменени с компонентите на вектора y:
В резултат на замяната получаваме:
След това можете да напишете векторната функция D(t,y):
Векторната функция D(t,y) има брой компоненти, равен на реда на диференциалното уравнение. Тъй като няма долни производни, вместо уравнения се записват техните обозначения (y1 и y2). Вместо най-голямата производна се записва дясната страна y3. Началните условия трябва да бъдат посочени за желаната функция и всяка долна производна, например:
Всяка от горните функции произвежда решение под формата на матрица с размер (m + 1) x (n + 1). Лявата му колона съдържа стойностите на аргумента t, разделящ интервала на еднакви стъпки, а останалите n колони съдържат стойностите на необходимите функции y0(t), y1(t), y2(t)…, изчислени за тези стойности на аргумента. Тъй като има m точки (в допълнение към първоначалната), ще има само m + 1 реда в матрицата на решението.
В повечето случаи е достатъчноизползвайте функцията rkfixed(), както е показано на фиг. 5.4 на примера за решаване на системата ODE на модела на затихналия осцилатор:
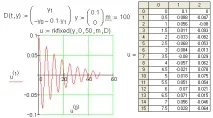
Ориз. 4.4. Решение на системата ODE от втори ред
Системата ODE на фиг. 5.4 се задава с помощта на векторната функция D(t, y), съставена съгласно описания по-горе метод. Векторът на началните стойности y има същия размер. Броят на стъпките, на които се определя решението, се задава с параметър m=100. Системата ODE се решава на интервала (0, 50). Можете да видите всички компоненти на матрицата, като използвате вертикалната лента за превъртане.
Често е по-удобно да се представят решения на обикновени диференциални уравнения не като функция на аргумента t, а във фазовото пространство. Фазовият портрет на системата е крива на фазовата равнина, построена в координатите y'(t) и y(t), фиг. 5.5.
Фазовият портрет, като правило, има една неподвижна точка (атрактор), върху която се "навива" разтворът. В теорията на динамичните системи атрактор от този тип се наричафокус.
Като цяло, ако системата се състои от n ODE, тогава фазовото пространство е n-мерно. За n>3 видимостта се губи и за да се визуализира фазовият портрет, трябва да се изградят неговите различни проекции.
Методът на Runge-Kutta от четвърти ред осигурява малка грешка за широк клас ODE системи, с изключение на твърдите системи. Следователно в повечето случаи си струва да използвате функцията rkfixed(). Ако по различни причини времето за изчисление стане критично или точността е незадоволителна, струва си да опитате други функции вместо rkfixed().
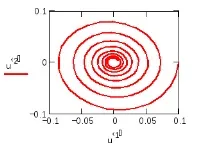
Ориз. 5.5. Фазов портрет на решението на системата ODE
Функцията Rkadapt() може да бъде полезна в случай, че е известно, че решението на разглеждания интервал варира малко или има сегментибавни и бързи промени. Методът Runge-Kutta с променлива стъпка разделя интервала не на еднакви стъпки, а по по-оптимален начин. Там, където решението се променя слабо, стъпките се избират по-рядко, а в областите на силните му промени - чести. В резултат на това са необходими по-малко стъпки за постигане на същата прецизност от rkfixed(). Методът Bulirsch-Stoer често е по-ефективен за намиране на гладки решения.