Книга: Скриптове за Blender 2.49

Гравиране

Помислете за следния проблем: даден текст, ние искаме да изобразим този текст като вдлъбнати канали на повърхността, точно както ако са гравирани. Не е толкова лесно, колкото изглежда. Разбира се, достатъчно е просто да създадете текстов обект, но за да манипулираме този текст, бихме искали да преобразуваме този текстов обект в мрежа. Интерфейсът на Blender предлага тази възможност в менюто на обекта, но колкото и да е странно, API на Blender не предоставя еквивалентна функция. Така че първата ни бариера ще бъде конвертирането на текстовия обект в мрежа.

Вторият проблем, който трябва да решим, е как да екструдираме набор от върхове или ръбове на правилната дълбочина от повърхността. Отново няма функция в API на Blender за това, така че трябва сами да го добавим към нашата кутия с инструменти.

Последният проблем е по-фин. Ако по някакъв начин сме успели да създадем някои вдлъбнати жлебове, може да искаме да направим ръбовете малко по-малко остри, тъй като нищо наистина няма абсолютно остри ръбове. Има различни начини да постигнете това, но много от тях включват добавяне на модификатор към нашата мрежа.Модификаторът за скосяване може да е достатъчен, за да премахне само острите ръбове, но вероятно бихме искали да добавим подповърхностен модификатор към цялата ни мрежа. Тук имаме проблем: когато запълваме празнините между знаците на нашия текст, е много вероятно да срещнем много тесни триъгълници. Тези триъгълници ще объркат външния вид на резултата от нашия подповърхностен модификатор, както можете да видите на следното изображение:

Две неща могат да помогнат за смекчаване на този проблем. Един едобавете тежест на гънките към ръбовете на нашия гравиран текст, като по този начин претегляте тези ръбове повече от изчислението на подповърхността по подразбиране. Това може да помогне, но също така може да ни отдалечи от целта на прилагането на модификатора, тъй като ще направи тези ръбове остри. Следващата снимка показва резултата: по-добър, но все още не перфектен.

Друг подход би бил да добавите допълнителен цикъл на линия точно извън гравирания текст. Това ще добави пръстен от четворни лица около текста, което прави подповърхността около текста да се държи много по-добре, както можете да видите по-долу. В нашата окончателна реализация ние прилагаме и двете решения, но първо ще се справим с всяка задача на свой ред.

Преобразуване на Text3d обект в мрежа

Обектът Text3d е базиран на крива с няколко допълнителни параметъра. Блокът от данни, за който се отнася, е обект на Blender Curve и след като знаем как да осъществим достъп до отделните части на кривата, които съставят всеки знак в нашия текст, можем да конвертираме тези криви във върхове и ръбове. Цялата подходяща функционалност може да бъде намерена в модулитеBlender.CurveиBlender.Geometry.

txt = ob.getData() curve = Blender.Curve.Get(txt.getName())

Сега можем да използваме txt за достъп до специфична за Text3d информация (напр. txt.setText('foo')) и curve за достъп до специфична за Curve информация (напр. curve.getNumCurves()).

Импортирайте блендер от blender.geometry import bezierinterp като interpolate от blender.mathutils emport vector as vec def curve2mesh (c): vlists = [] За CN в C: npoints = len (cn) точки = [] first за сегмент вдиапазон(npoints-1): a=cn[сегмент].vec b=cn[сегмент+1].veclastpoints = interpolate(vec(a[1]),vec(a[2]),vec(b[0]), vec(b[1]),6) ако първо: first = False точки. append(lastpoints[0]) points.extend(lastpoints[1:])if cn.isCyclic(): a=cn[-1].vec b=cn[0].vec lastpoints=interpolate(vec(a[1]), vec(a[2]), vec(b[0]), ve c(b[1] ),6) points.extend(lastpoints[:-2]) vlists.append(points) върни vlists

Маркираните редове показват два важни аспекта. Първият показва действителната интерполация. Преименувахме доста тромавата функцияBezierInterp()наinterpolate()и тя приема пет аргумента. Първите четири са взети от дватаBezTripleобекта, между които интерполираме. Във всекиBezTripleобект може да бъде достъпен списък от три вектора: входящ манипулатор, позиция на точка и изходящ манипулатор (вижте следващата фигура). Преминаваме позицията на първата точка и изходящата дръжка и позицията на втората точка и входящата дръжка. Петият аргумент е броят точки, които искаме да изведем от функциятаinterpolate().

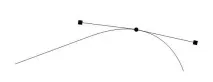
Вторият маркиран ред се грижи зазатворени криви - криви, където първата и последната им точка са свързани. Такъв е случаят с всички криви, които образуват знаци в текста. Функцията връща списък със списъци. Всеки списък съдържа всички интерполирани точки (кортежи от координати x, y, z) за всяка крива. Имайте предвид, че някои символи са съставени от повече от една крива. Например малката буква e в много шрифтове или буквата o се състои от две криви, едната определя външната граница на буквата и една вътрешна. ОбектътText3d, съдържащ текстаFoo, например, връща списък спет списъка - първият ще съдържа върховете, които определят голямата букваF, а вторият и третият ще съдържат върховете за двете криви, които създават малката буква o, също и четвъртият и петият.

Цикъл на екструдиране на ребра

Екструзията е процес, при който дублираме върхове (и евентуално ръбовете, които ги свързват) и ги преместваме в някаква посока, след което свързваме тези дублирани върхове с техните оригинали с нови ръбове и завършваме операцията, като създаваме ново лице между стария и новите върхове. Имаме нужда от това, за да потънем очертанията на нашия текст, за да създадем жлеб с вертикални стени. Функциятаextrude_selected_edges()вTools.pyприема мрежа и вектор като аргументи и ще екструдира върховете на избраните ръбове в мрежата в посока на вектора, добавяйки всички необходими нови ръбове и лица. Тъй като тази техника е разширение на това, което сме виждали преди, кодът не е показан тук.

Разширяване на редов цикъл

Ако имаме списък с ръбове, които образуват затворена крива (или повече от една), дефинираща символ, бихме искали да заобиколим тези ръбове с допълнителен контур на ръба, за да създадем по-добро „изпълнение“ на всеки подповърхностен модификатор, който крайният потребител може да свърже с нашата мрежа. Това би бил доста сложен процес, ако трябваше да го изчислим в 3D, но за щастие нашите преобразувани символи имат всичките си върхове в равнината xy (това е така, защото всички знаци в новите екземпляри на обекта Text3d лежат в равнината xy).

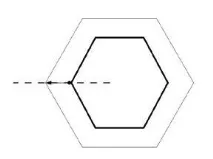
Само две измерения са доста ковък проблем. За всяка точка в нашия ръбов цикъл ние определяме посоката на нормалата на върха.Пикnormal е линия, която пресича наполовина ъгъла между два ръба, които разделят точката, която разглеждаме. Ако два ръба са колинеарни (или почти такива), приемаме линията, перпендикулярна на един от ръбовете, като нормала на върха. Позицията на точката, създадена в новия проводник, ще бъде някъде на тази нормала. За да решим дали трябва да се движим навън или навътре по тази нормала, ние просто опитваме една посока и проверяваме новата позиция, за да видим дали е в границите на нашия символ. Ако е така, поемаме в обратната посока.

Един проблем все още трябва да бъде решен: един символ може да се състои от повече от една крива. Ако искаме да направим допълнителни линейни цикли около такъв символ, такъв ръбов цикъл трябва да бъде извън външната граница на знака, но вътре във всяка вътрешна крива. С други думи, ако създадем нов ръбов цикъл, трябва да знаем дали една крива лежи вътре в друга крива. Ако е така, тогава това не е външна граница и новият ръбов цикъл трябва да бъде създаден, разположен вътре в кривата. Следователно нашата функцияexpand()(показана в следния кодов фрагмент, пълният код е част от Tools.py. Всъщност тази и всички функции, които извиква, са в expand.py - прибл. Lane), приема допълнителен незадължителен аргументplist, който е списък от списъци, съдържащиMVertобекти, които дефинират допълнителни полигони за проверка . Ако първата точка от кривата, която искаме да разширим, се намира в някоя от тези допълнителни криви, приемаме, че кривата, която разширяваме, евътрешна крива. (Това ще бъде неправилно предположение, ако вътрешната крива пресича външната крива в даден момент, но за криви, определящизнак в шрифт, това никога не се случва.)

def expand(me,loop,offset=0.05,plist=[]):ov = [me.verts[i] for i in verts_from_edgegeloop(loop)] ins > за многоъгълник в plist: if in_polygon(loop[0].v1.co,polygon): ins > прекъсване # нямаме работа с множество включвания n=len(ov) points=[] for i in range(n): va = (ov[i].co-ov[(i+1)%n].co).normalize() vb = (ov[i].co-ov[(i-1)%n].co).normalize() cosa=abs(vec(va).dot( vb )) if cosa>0.99999 : # почти колинеарно c = vec(va[1],va[0],va[2]) else: c = va+vb l = отместване/c.length p = ov[i].co+l*c if in_polygon(p,ov) != вътре: p = ov[i].co-l*c print i,ov[i].co,va,vb,c,l,cosa,p points.append(p) return points

Маркираният код извиква функция (предоставена вTools.py), която взема списък от ръбове, които образуват ръбов цикъл, и връща сортиран списък от върхове. Това е необходимо, защото нашата функцияin_polygon()взема списък от върхове, а не ръбове, и предполага, че списъкът е сортиран, тоест съседни върхове образуват ръбове, които не се пресичат.

За да определим дали дадена точка е вътре в затворен многоъгълник, дефиниран от списък от върхове, ние преброяваме броя на ръбовете, които се пресичат от линия (често наричаналъч ), която започва в дадена точка и се простира до безкрайност. Ако броят на пресечените ръбове е нечетен, точката се намира вътре в многоъгълника; ако е четен, той се намира извън многоъгълника. Следната фигура илюстрира концепцията: